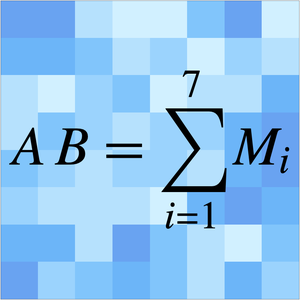Comparez les algorithmes en utilisant les relations asymptotiques
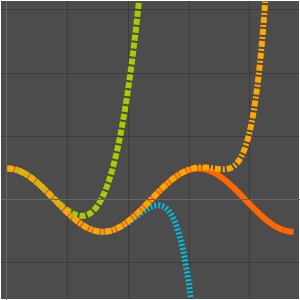
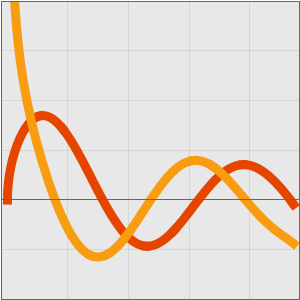
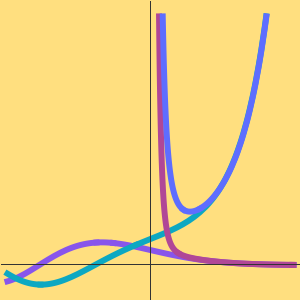
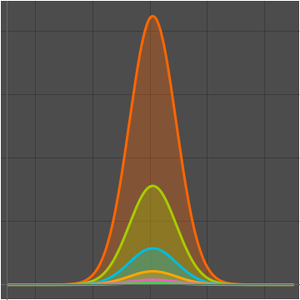
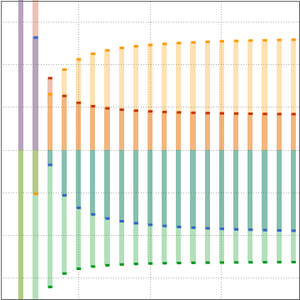
Dans la complexité de calcul, les algorithmes sont classés par leur comportement dans les entrées volumineuses, généralement considérées comme infinies. Deux algorithmes sont comparés si le temps d'exécution de l'un est AsymptoticLessEqual (grand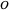 
), AsymptoticLess (petit 
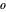), AsymptoticGreaterEqual (grand 
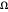) ou AsymptoticGreater (petit 
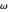) par rapport au temps d'exécution de l'autre.
Le problème des vendeurs itinérants (PVI) consiste à trouver l'itinéraire le plus court reliant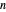 
villes. Un algorithme naïf consiste à essayer tous les itinéraires 
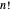. L'algorithme Held-Karp améliore cela d'environ 
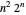étapes. Démontrez que 
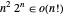et donc que l'algorithme Held-Karp est plus rapide.
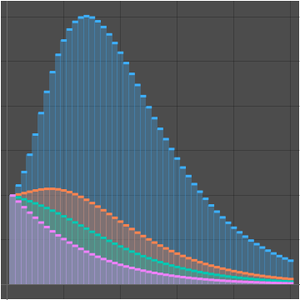
Les deux algorithmes démontrent que la classe de complexité de PVI n'est pas pire que celle de EXPTIME dont les problèmes peuvent être résolus pour le temps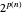 
. Par exemple, 
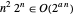pour 
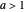, l'algorithme Held-Karp a donc un temps d'exécution exponentiel.
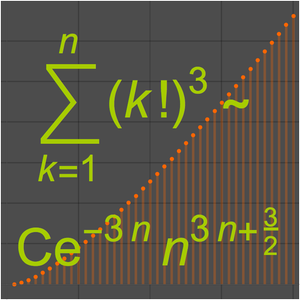
Pour la fonction factorielle, une exponentielle linéaire ne suffit pas parce que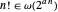 
.
Cependant, une factorielle a toujours une durée d'exécution exponentielle parce que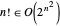 
.
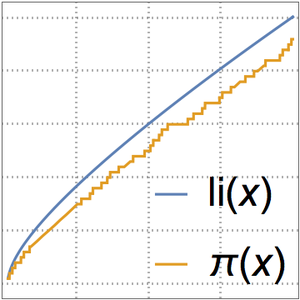
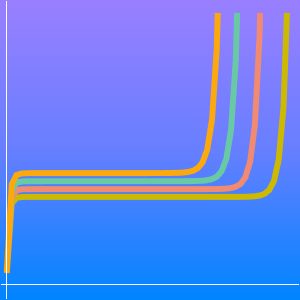
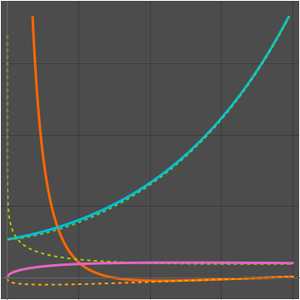
Des solutions approximatives peuvent être trouvées pour le temps 
, de sorte que le PVI approximatif se situe dans la classe de complexité P des problèmes qui peuvent être résolus dans le temps polynomial. Tout algorithme polynomial est plus rapide qu'un algorithme exponentiel, ou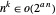 
.
