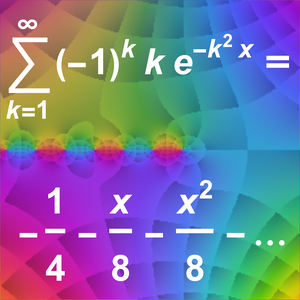Generate an Asymptotic Expansion (AsymptoticDSolveValue)
A linear ordinary differential equation can be approximated by general asymptotic series 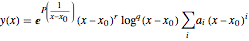 near an irregular singular point for the equation. This example shows how to obtain such an approximation using AsymptoticDSolveValue. The exponential factor in the asymptotic series is required to capture the rapid growth, decay or oscillation of the solution near the irregular singular point.
near an irregular singular point for the equation. This example shows how to obtain such an approximation using AsymptoticDSolveValue. The exponential factor in the asymptotic series is required to capture the rapid growth, decay or oscillation of the solution near the irregular singular point.
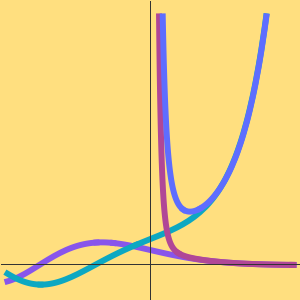
Find an asymptotic approximation for a linear first-order ODE at the irregular singular point 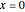 .
.
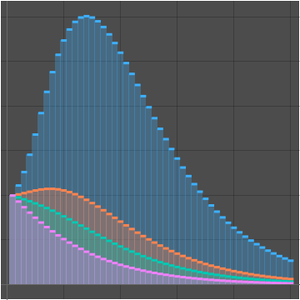
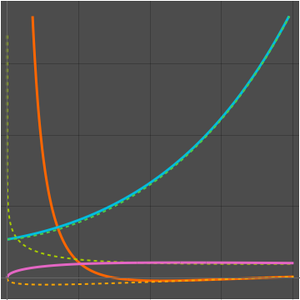
Plot the successive approximations given by the solution.
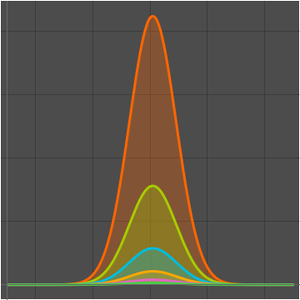
The Airy equation has an irregular singular point at 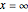 .
.
Compute an asymptotic expansion at the irregular singular point.
Comparing with the series at Infinity of the standard Airy function 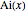 shows that it corresponds to the choice
shows that it corresponds to the choice 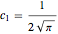 ,
, 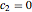 .
.
The function 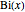 corresponds to the choice
corresponds to the choice 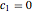 ,
, 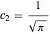 .
.
For values of 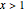 , the asymptotic expansion rapidly gives an excellent approximation.
, the asymptotic expansion rapidly gives an excellent approximation.
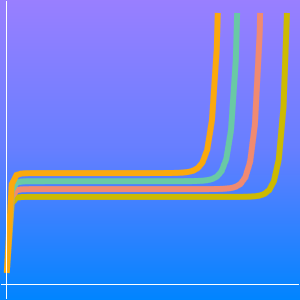
Find an asymptotic approximation for a linear higher-order ODE at the irregular singular point 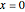 .
.