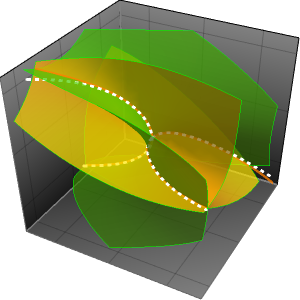
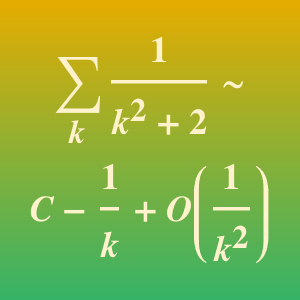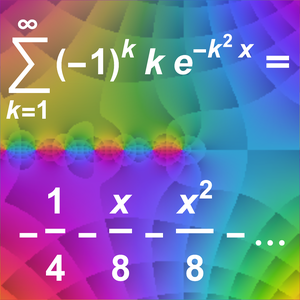Eine asymptotische Entwicklung generieren (AsymptoticDSolveValue)
Eine lineare gewöhnliche Differentialgleichung kann durch allgemeine asymptotische Reihen 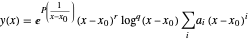 bei einem für die Gleichung irreegulären singulären Punkt approximiert werden. Dieses Beispiel zeigt, wie man eine solche Näherung mit AsymptoticDSolveValue erhält. Der Exponentialfaktor in der asymptotischen Reihe ist erforderlich, um das schnelle Wachstum, den Zerfall oder die Schwingung der Lösung bei dem irregulären singulären Punktes zu erfassen.
bei einem für die Gleichung irreegulären singulären Punkt approximiert werden. Dieses Beispiel zeigt, wie man eine solche Näherung mit AsymptoticDSolveValue erhält. Der Exponentialfaktor in der asymptotischen Reihe ist erforderlich, um das schnelle Wachstum, den Zerfall oder die Schwingung der Lösung bei dem irregulären singulären Punktes zu erfassen.
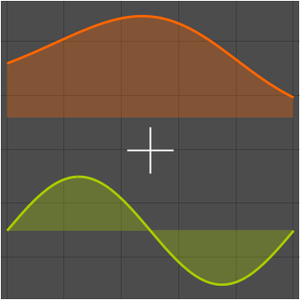
Ermitteln Sie eine asymptotische Approximation für eine lineare GDG erster Ordnung beim irregulären singulären Punkt 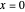 .
.
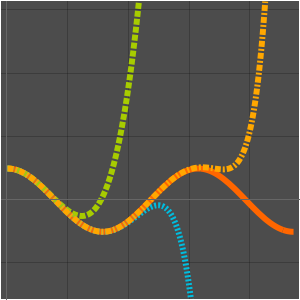
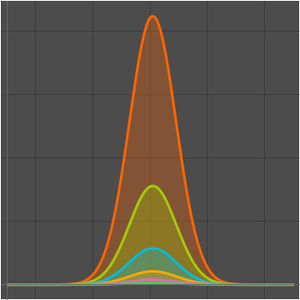
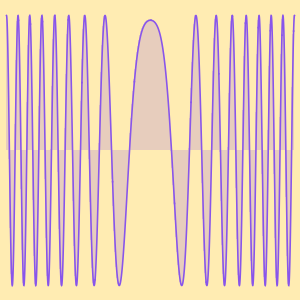
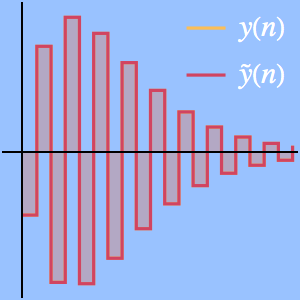
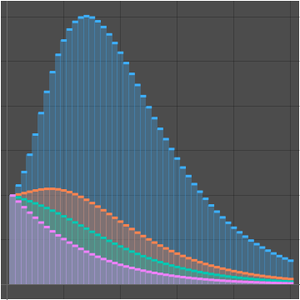
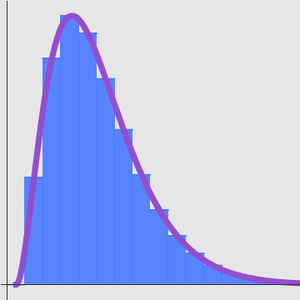
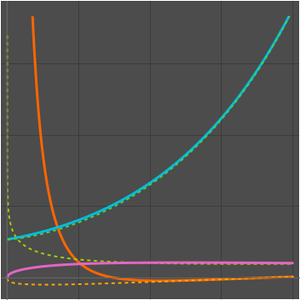
Plotten Sie die aufeinanderfolgenden Näherungen, die durch die Lösung gegeben sind.
Die Airy-Gleichung hat einen irregulären singulären Punkt bei 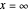 .
.
Berechnen Sie eine asymptotische Entwicklung beim irregulären singulären Punkt.
Der Vergleich mit der Reihe bei Infinity der standardmäßigen Airy-Funktion 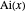 zeigt, dass sie
zeigt, dass sie 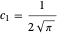 ,
, 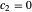 entspricht.
entspricht.
Die Funktion 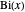 entspricht
entspricht 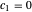 ,
, 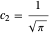 .
.
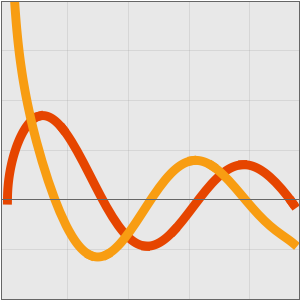
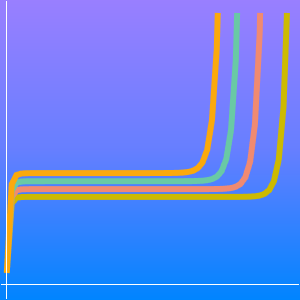
Bei Werten von 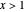 liefert die asymptotische Entwicklung eine exzellente Approximation.
liefert die asymptotische Entwicklung eine exzellente Approximation.
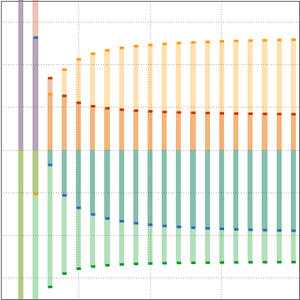
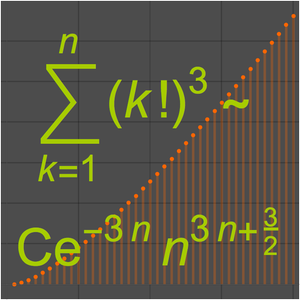
Ermitteln Sie eine asymptotische Approximation für eine lineare GDG höherer Ordnung am irregulären singulären Punkt 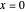 .
.