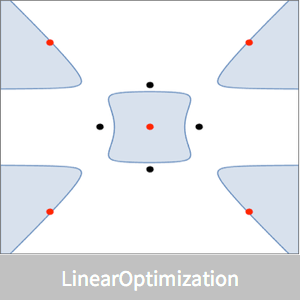
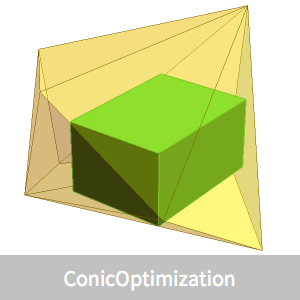
最大体積の立方体
凸多面体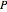 
に内接する，最大体積の軸平行の直方体を求める．
この例では，正項の積の最適化をpower cone制約条件で表す方法を説明する．この制約条件をConicOptimizationと一緒に使って最適条件を求めることができる．
ランダムな点の凸包として構築されたランダムな凸多面体を考える．
直方体をWolfram言語の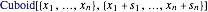
で表すために，直方体の底面のコーナー 
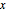と辺長 
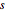のベクトルを求める．直方体の体積は辺長の積であるから，目的は 
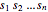を最大化することである．直方体のすべてのコーナーが 
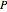の中に収まれば，直方体の点もすべて収まる．コーナーは 
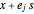で表される．ここで 
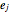は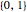
からの可能な n 組の要素すべての集合 
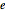にある．
問題は以下のようになる．
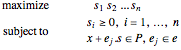
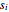は非負なので，積 
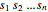を最大化することは幾何平均
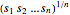（凹形となることが分かっている）を最大化することに等しい．
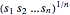を最大化することは，
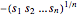（凸形）を最小化することに等しい．補助変数 
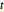を使うと，追加の制約条件
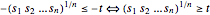を持つ線形目的関数-
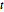でこの問題を再定式化することができる．
この問題は以下のようになる．
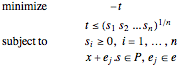
power coneは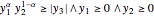 
となるような 
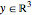の集合であり，Wolfram言語の
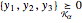で表すことができる．
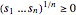であるため，新しい制約条件
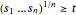は非負の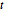 
について満足し，
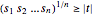に等しい．これは，以下の一連のpower cone制約条件で書くことができる．
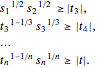
のとき，問題は以下のようになる．
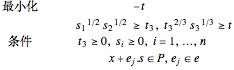
凸多面体は半空間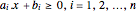 
の交点として表すことができる．各辺の係数
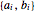を抽出する．
問題を解く．
最大体積の内接する直方体を表示する．
多面体の代りに，凸錘で表現可能な集合K⊆n（楕円体等）を取ることができる．直方体の頂点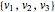
は，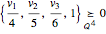
のとき，かつそのときに限り楕円体の内部にある．
問題を解く．
結果をプロットする．
