構造最適化問題
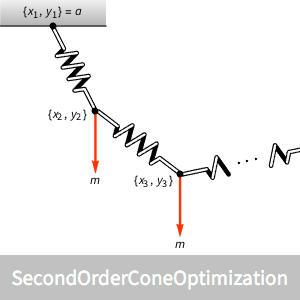
リンクの各接合点に質量がある，いくつかのバネリンクによって形成される吊り下げ鎖の形状を求める．
この例では，平衡についての最小のエネルギー状態を，二次錐（ノルム）制約条件下の最適化問題で表す方法を示す．これはSecondOrderConeOptimizationで簡単に解くことができる．
各リンクの端点の垂直荷重のもとで 
個のバネリンクによって形成される吊り下げ鎖の形状を求める．目的は，両端の位置が 
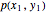および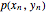 
である場合のリンクの位置 
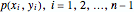を求めることである．
バネの重さを無視した，重力によるポテンシャルエネルギーは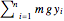
である．ここで 
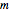は各端点における垂直荷重， 
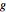は標準重力である．
伸長によってかかるバネリンクの張力によるポテンシャルエネルギーは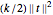
である．ここで 
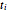はバネリンク 
の伸長，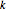
はバネの硬さである．
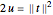を使うと，エネルギーは 
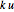に変換される．
この変換のために追加の制約条件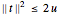 
を加えなければならない．
リンクされた鎖の端点は位置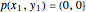 
と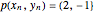 
で固定される．
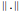は凸なので，各バネが条件
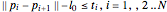を満足するだけで十分である．ここで 
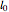は，各バネの静止長である．
設計パラメータは以下である．
最終的な目的関数は，最小化されなければならない重力とバネポテンシャルエネルギーの和である．
各バネリンクの端点を求める．
結果のバネ鎖の形状を可視化する．
伸長はリンク鎖の端に近いリンクで大きくなっている．リンク11と12の伸長が最も小さい．
解は，リンクの数や端点を操作するのに十分な速さである．
