最適な平面計画
個の小さい長方形を，最小の外周を持つより大きい長方形の中に配置する問題を考える．ここで，相対的な配置，縦横比，間の間隔，小さい長方形の面積についての制約がある．
この例題は，NMinimizeを使う関数の定義にWolfram言語を使って，平面計画問題を解くものである．この関数は半定値不等式を含む，ベクトル不等式を使う．
大きい方の長方形をRectangle[{0, 0}, {H, W}]で，小さい長方形のそれぞれを ri=Rectangle[{xi, yi}, {xi+wi, yi+hi}], i=1 … n で記述する．
相対的な配置は，水平方向の配置と垂直方向の配置の2つの有向グラフで表すことができる．辺 ij があるとすると，ri は rj の左（あるいは下）である．
簡単にするために，すべての長方形の縦横比は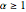 
では
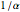と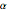 
の間であり，長方形同士の間隔は 
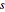とする．
これらの入力と小さい長方形の面積のリストが与えられると，最小外周を持つ大きい長方形を求める関数planFloorを定義することができる．
完全なWolfram言語入力を表示する
10個の小さい長方形の相対的な配置のためのグラフを設定する．
小さい長方形のうちの1個だけは面積400で，残りはすべて100となるようにする．
以下により平面計画を最適化する．
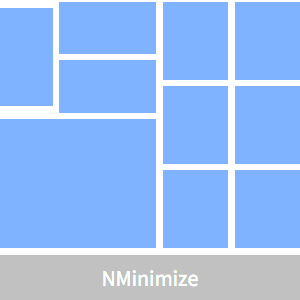
最適な計画を表示する．
以下は，面積の制約が満足されていることを示す．
面積がランダムであるときの配置を比較する．
