最大カット問題
最大カット問題とは，部分集合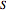 
からその補集合 
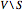までを横断する辺の重み 
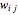の総和が最大になるようなグラフの頂点 
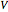の部分集合 
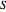を求めるものである．
この例題では，SemidefiniteOptimizationを使ってNP完全の最大カット問題の緩和を効率的に解く関数を設定する方法を示す．
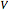が 
個の頂点を持ち，その頂点が指標
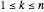で表されるとする．
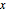を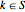 
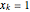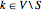のとき 
，
のとき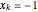 
の要素を持つベクトルとし，
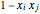は 
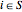かつ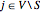 
の場合にのみ非零(=2)になるようにする．したがって，最大カットは
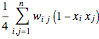を最大化することで求められる．ここで 
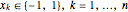である．目的は
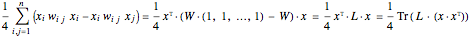
として書き換えることができる．ここで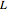 
はグラフのラプラシアン(Laplacian)行列，
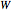は重み付きの隣接行列である．
小さいグラフの場合は最大カット問題は厳密に解くことができるが，大きいグラフになると，一般に問題にNP完全性が含まれるため，実行が難しい．
この問題は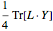
を最小化する．ここで 
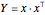はランク1の対称な半正定値行列であり，それぞれの 
について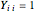
である．これ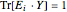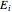は，
（
は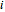 
番目の対角位置が1，その他はどこでも0である行列）と同等である．
解を実践的なものにするために，緩やかな問題を解いてみる．ランク1の条件が排除されたので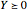 
しか必要ではない．
双対形式の半定値問題は以下で与えられる．
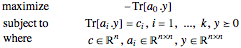
これはSemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }]を使って解かれる．
緩和問題の解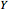 
では，カットはランダム化された丸めにより構築される．
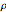を単位ノルムの一様分布に従うランダムベクトルとし，
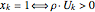として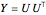 
を分解する．例示のために，緩和値，丸められた値，赤で示された 
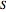の頂点を含むグラフを示す関数が定義される．
先に示した方法を使って最大カットの近似を求め，厳密な結果と比較する．
格子グラフの最大カットを求める．
ランダムグラフの最大カットを求める．
ピーターセン(Peterson)グラフでの緩和アルゴリズムと厳密なアルゴリズムでかかる時間を比較する．
