Cubóide de volume máximo
Encontre o cubóide de eixo paralelo de volume máximo inscrito em um poliedro convexo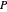 
.
Este exemplo monstra como a otimização de um produto de termos positivos pode ser expressa em termos de restrições de cone de energia que podem ser usadas com ConicOptimization para encontrar o melhor.
Considere um poliedro convexo aleatório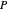 
construído como o casco convexo de pontos aleatórios.
Para o cubóide, encontre um ponto de canto inferior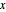 
e um vetor de comprimento lateral 
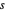de modo que o cubóide seja representado na Wolfram Language por 
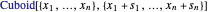. O volume do cubóide é apenas o produto dos comprimentos laterais, então o objetivo é maximizar 
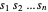. Se todos os cantos do cubóide estão em 
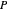, então todos os pontos no cubóide também estão. Os cantos podem ser descritos por 
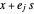, onde 
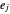está no conjunto 
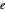de todas as possíveis n‐tuplas de elementos de 
.
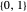O problema se torna:
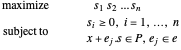
Como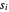 
não é negativo, maximizando o produto de 
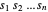é o mesmo que maximizar a média geométrica de 
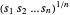, que é côncavo. Maximizar 
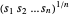é equivalente a minimizar 
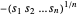, que é convexo. Usando uma variável auxiliar 
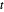, reformule o problema com uma função objetiva linear -
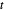com as restrições adicionais 
.
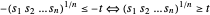O problema se torna:
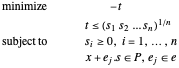
O cone convexo é o conjunto de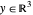 
de modo que 
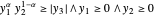, e pode ser expresso na Wolfram Language por 
.
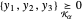Como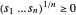 
, a nova restrição 
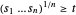pode ser satisfeita para 
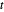não-negativo e é equivalente a 
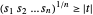. Isso pode ser escrito como uma série de restrições do cone convexo.
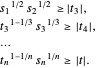
Para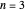 
o problema se torna:
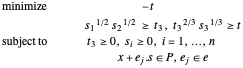
Um poliedro convexo pode ser representado como interseções de meio-espaços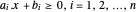 
. Extraia os coeficientes 
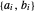para cada lado.
Resolva o problema.
Mostre o cubóide com o máximo volume inscrito.
Em vez de um poliedro, pegue qualquer conjunto representável cônico convexo K⊆n—por exemplo, um elipsóide. Um vértice do cubóide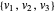 
está dentro do elipsóide se 
.
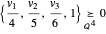Resolva o problema.
Faça uma ilustração do resultado.
