Wolfram Language™

Planejamento de piso ideal

Considere o problema de colocar 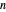retângulos menores dentro de um retângulo maior de perímetro mínimo com restrições no posicionamento relativo, razão de aspecto, espaçamento e área de retângulos menores.

Este exemplo monstra o uso da Wolfram Language para definir uma função que usa NMinimize para resolver problemas de planejamento de piso. A função usa desigualdades de vetor, incluindo uma desigualdade semidefinida.

Descreva o retângulo maior por Rectangle[{0, 0}, {H, W}] e cada um dos menores por r_i=Rectangle[{x_i, y_i}, {x_i+w_i, y_i+h_i}], i=1 … n .

O posicionamento relativo pode ser descrito por dois gráficos direcionados, um para posicionamento horizontal e outro para posicionamento vertical. Se tiver uma borda ij, então r_i deve estar à esquerda de (ou abaixo) r_j.

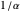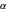Para simplificar, assuma que todos os retângulos devem ter uma proporção entre e para 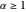e que o espaçamento entre retângulos é .

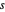Dados estes inputs e uma lista das áreas dos retângulos menores, você pode definir uma função planFloor que encontra o perímetro mínimo do retângulo maior.

Configure gráficos para o posicionamento relativo de 10 retângulos menores.

Determine que as áreas de todos os retângulos menores sejam 100, exceto uma que tenha área 400.

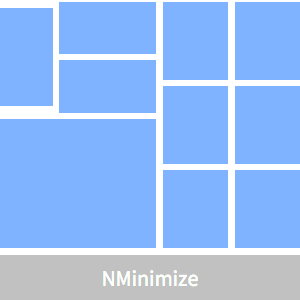
Isso otimiza o planejamento do piso.

Mostre o plano ideal.

Isso mostra que a restrição de área está satisfeita com a igualdade.

Compare os layouts quando as áreas são feitas aleatoriamente.