Wolfram Language™

Design de treliça ideal

Projete uma treliça de peso mínimo ancorada em uma extremidade à parede e que deve suportar uma carga na outra extremidade.

Este exemplo monstra quantos recursos da Wolfram Language podem ser usados juntos para formar uma forma simbólica de um problema de otimização linear que pode ser resolvido de forma eficiente com LinearOptimization.

Selecione algumas posições específicas onde a treliça está ancorada na parede.

A posição onde a carga é aplicada é no final da treliça.

A treliça pode ser modelada usando conexões e nós. Cada nó está conectado a um nó vizinho por uma conexão. Um possível padrão de conectividade é dado aqui.

Os nós candidatos são colocados em uma estrutura retangular.

Visualize as posições dos nós, as posições dos pontos de ancoragem, a posição onde a força é aplicada e a conectividade de um único nó no meio da treliça.

Cada nó está associado a um índice exclusivo. Association fornece de forma eficiente uma tabela de pesquisa rápida.

Encontre os índices associados à âncora e pontos de aplicação das forças.

Construa uma função que forneça a conectividade de qualquer ponto de rede para qualquer padrão de conectividade fornecido.

Para um determinado nó 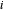, use a conectividade para determinar quais ligações incluem esse nó. Se os nós 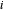e 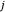estão conectados, então 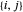e 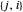representam o mesmo link. Para evitar a repetição, considere apenas aquele com .

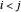Descreva o conjunto de links por ℒ de modo que, se o nó 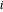e o nó 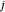formam um link, então .

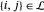Suponha que a espessura de uma conexão e, portanto, a massa por unidade de comprimento, precisa ser proporcional à força que será exercida naquela conexão. Uma maneira conveniente de descrever as conexões em ℒ é ter uma indexação de conexões para que, para cada par conectado 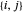, existe um índice único 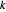com .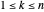

O objetivo é minimizar 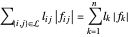, onde 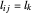é o comprimento da conexão entre nós 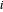e 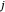com o índic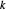e e 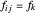é a força exercida pela conexão nas suas juntas finais.

A função 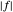é não linear, mas pode ser expressa como uma função linear, introduzindo 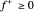e 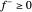de modo qu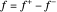e e 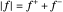. O objetivo é .

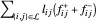Em cada nó, exceto no ponto de força, não há forças externas aplicadas.

No ponto de força, há uma força unitária descendente vertical aplicada.

Em cada nó não ancorado 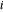, deve haver um equilíbrio de forças 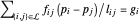, onde 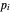é a posição do nó 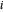e 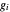é a força externa no nó 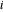. Defina uma função que forneça a restrição de equilíbrio de força para o nó .

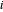Use Complement para evitar incluir os nós âncora.

As restrições finais são:

Resolva o sistema resultante.

Visualize a treliça ideal com tons de azul indicando compressão de conexões e tons de vermelho indicando expansão de conexões.