Problema de atribuição ideal
Calcule a quantidade de energia que uma empresa precisa enviar de suas quatro usinas para cinco cidades para maximizar os lucros e minimizar os custos, atendendo ao pico de demanda nas cidades.
Este exemplo mostra como a LinearFractionalOptimization pode ser usada para minimizar a relação custo-benefício dentro de certos limites. Usar uma variável com valor de matriz torna a modelagem relativamente fácil.
Use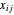 
para representar a quantidade de eletricidade enviada pela planta 
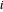para a cidade 
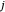. O custo total do transporte de eletricidade é 
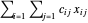, onde 
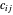é o custo de transportar eletricidade da planta 
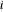para a cidade 
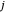. Total[m, 2] dá o total de todos os elementos de uma matriz 
.
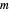O lucro total feito pela empresa de energia é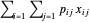 
, onde 
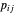é o lucro obtido pela planta 
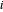vendendo eletricidade para a cidade 
.
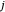A eletricidade total enviada por cada usina é dada por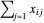 
e deve ser maior ou igual ao mínimo de eletricidade que a usina pode fornecer. Total[x, {2}] dá o total para cada linha de 
.
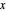A eletricidade total enviada para cada cidade é dada por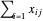 
e deve ser maior que a demanda mínima e menor ou igual à demanda de pico. Total[x, 1]dá o total das colunas de 
.
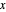As plantas só podem dar e não receber energia das cidades. VectorGreaterEqual pode ser usado para indicar que todos os elementos das variáveis da matriz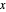 
devem ser maiores ou iguais a zero.
Como exemplo, aqui está o custo de transportar um milhão de quilowatts-hora (kWh) de eletricidade de quatro usinas para cinco cidades.
O lucro que cada usina gera ao vender 1 milhão de kWh para cada cidade é mostrado aqui.
As cidades têm demanda máxima de 45, 20, 30, 30 e 40 milhões de kWh, respectivamente, e uma demanda mínima de 5 milhões de kWh.
As usinas podem fornecer um mínimo de 35, 50, 40 e 40 milhões de kWh de eletricidade, respectivamente.
A quantidade ideal de eletricidade para enviar cada cidade por planta pode ser encontrada minimizando a relação entre o custo e o lucro.
A distribuição da eletricidade fornecida é mostrada abaixo.
