Otimização de trajetória
Minimize 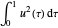 sujeito a
sujeito a 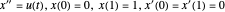 .
.
Este exemplo monstra como um problema variacional pode ser discretizado para um problema de otimização finita resolvido de forma eficiente por métodos convexos, como QuadraticOptimization.
O problema variacional será aproximado discretizando o problema do valor limite e usando a regra trapezoidal para integrar em uma grade uniformemente espaçada no intervalo [0,1], 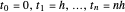 com
com 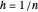 .
.
Use a variável u[i] para representar 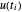 e x[i] para representar
e x[i] para representar 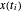 para
para 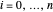 .
.
A restrição de equação diferencial é facilmente representada usando aproximações centradas de diferença de segunda ordem para 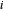 de 1 a
de 1 a 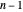 .
.
No limite, as condições de derivação zero permitem o uso de pontos fictícios 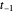 e
e 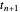 . Quando
. Quando 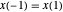 e
e 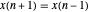 , a fórmula de diferença de segunda ordem para o primeira derivada
, a fórmula de diferença de segunda ordem para o primeira derivada 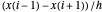 é zero para
é zero para 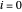 e
e 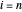 . Assim, no limite, use o seguinte.
. Assim, no limite, use o seguinte.
A regra trapezoidal para 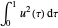 é dada conforme abaixo.
é dada conforme abaixo.
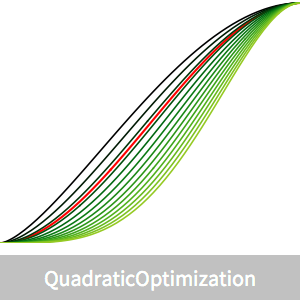
Como a expressão da regra trapezoidal é quadrática e todas as restrições são restrições de igualdade linear, o mínimo da integral discretizada pode ser encontrado usando QuadraticOptimization diretamente.
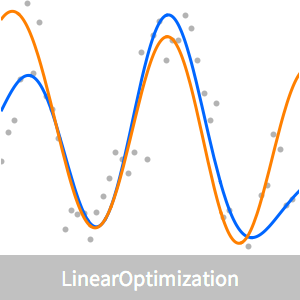
Funções aproximadas são construídas com Interpolation.
Uma solução analítica exata, 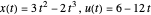 , é conhecida por este problema, por isso é possível representar o erro na discretização.
, é conhecida por este problema, por isso é possível representar o erro na discretização.
O erro assintótico é aproximadamente 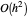 , então dobrando
, então dobrando 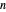 para 200 e recalculando, o erro será cerca de 1/4 do que é mostrado aqui.
para 200 e recalculando, o erro será cerca de 1/4 do que é mostrado aqui.
A solução analítica pode ser encontrada considerando uma família de curvas 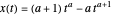 onde
onde 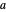 é um parâmetro. Esta curva paramétrica satisfaz as condições de contorno prescritas
é um parâmetro. Esta curva paramétrica satisfaz as condições de contorno prescritas 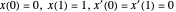 . Como
. Como 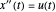 , pode-se encontrar um parâmetro ideal
, pode-se encontrar um parâmetro ideal 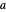 que minimize
que minimize 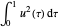 .
.
O valor ideal de 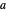 está em 2, que é o resultado analítico
está em 2, que é o resultado analítico 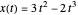 .
.