Otimização dos autovalores
Encontre combinações lineares de matrizes simétricas que otimizam várias propriedades relacionadas aos autovalores das combinações.
Este exemplo demonstra como as restrições semidefinidas (que são efetivamente restrições de autovalores) podem ser usadas de maneiras diferentes com SemidefiniteOptimization para resolver problemas de otimização de autovalores.
Encontre 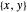 que minimiza o maior autovalor de uma matriz simétrica
que minimiza o maior autovalor de uma matriz simétrica 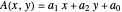 .
.
O problema pode ser formulado como uma desigualdade matricial linear uma vez que 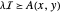 é equivalente a
é equivalente a 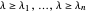 , onde
, onde 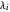 é o
é o 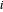 th autovalor de
th autovalor de 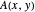 .
.
Construa a matriz com o autovalor máximo.
Calcule seus autovalores.
Ilustre a solução em um gráfico de autovalor máximo como uma função de 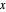 e
e 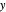 .
.
Execute uma simulação de Monte Carlo para verificar a razoabilidade do resultado.
Resolva alguns problemas semelhantes. Maximize o menor autovalor.
Minimize a diferença entre o maior e o menor autovalor.
Minimize o maior autovalor pelo autovalor de valor absoluto (ou a norma espectral).
Em princípio, isso funciona para uma combinação de qualquer número de matrizes de qualquer tamanho.