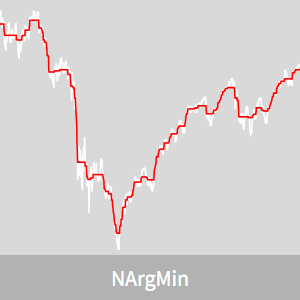
Suavização de preservação de estrutura
A regularização de ajuste de variação total pode ser usada para filtrar o ruído em um sinal enquanto, ao mesmo tempo, preserva saltos que são significativos.
Este exemplo monstra como a modelagem direta em termos das funções da Wolfram Language pode ser usada para implementar a regularização total do ajuste de variação de maneira natural usando NArgMin.
Para um sinal 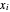 , isso é feito encontrando valores
, isso é feito encontrando valores 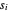 que minimizam
que minimizam 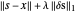 , onde
, onde 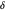 s é o vetor com elementos
s é o vetor com elementos 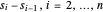 e λ é um parâmetro usado para trocar entre a redução de ruído e a proximidade do sinal
e λ é um parâmetro usado para trocar entre a redução de ruído e a proximidade do sinal 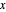 .
.
Considere o índice de ações Dow Jones Industrial Average durante a crise financeira de 2008. Há muita volatilidade no dia-a-dia que, a longo prazo, pode efetivamente ser considerada ruído.
O sinal é a sequência de valores do índice de ações.
Encontre o índice suavizado para 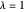 . Method->"Convex" é usado porque outros métodos seriam muito lentos se fossem realmente bem sucedidos para essas variáveis.
. Method->"Convex" é usado porque outros métodos seriam muito lentos se fossem realmente bem sucedidos para essas variáveis.
Compare o índice suavizado com o índice real.
O índice suavizado mostra as principais tendências, mas perde algumas características importantes. Existe uma compensação entre os recursos de captura e quanta suavização é feita que é determinada por 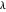 . Para
. Para 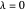 , não há suavização e
, não há suavização e 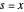 . Por outro lado, como
. Por outro lado, como 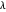 se aproxima de ∞,
se aproxima de ∞, 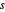 vai se aproximar de um sinal constante. Um gráfico da variação total em relação ao desvio do sinal original para diferentes valores de
vai se aproximar de um sinal constante. Um gráfico da variação total em relação ao desvio do sinal original para diferentes valores de 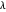 pode dar uma indicação de valores apropriados de
pode dar uma indicação de valores apropriados de 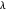 para alcançar o melhor equilíbrio.
para alcançar o melhor equilíbrio.
Há uma dobra perceptível na curva ao redor de 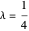 , indicando que isso alcança um equilíbrio razoável.
, indicando que isso alcança um equilíbrio razoável.
É interessante observar o índice suavizado para alguns dos diferentes valores de 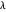 .
.
A minimização também pode ser pensada em termos de ajuste de mínimos quadrados com regularização. A nova opção FitRegularization pode ser usada em Fit para fazer isso.