Routenoptimierung
Minimieren Sie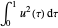 
unter den Nebenbedingungen 
.
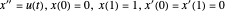Dieses Beispiel zeigt, wie ein Variationsproblem zu einem endlichen Optimierungsproblem diskretisiert werden kann, das durch konvexe Methoden, wie z.B. QuadraticOptimization effizient gelöst wird.
Das Variationsproblem wird durch Diskretisierung des Randwertproblems und unter Verwendung der Trapezregel zur Integration in ein Raster mit einheitlichen Abständen im Intervall [0,1],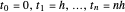 
mit 
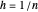approximiert.
Die Variable u[i] repräsentiert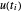 
und x[i] repräsentiert 
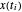für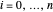 
.
Die Einschränkung der Differentialgleichung lässt sich leicht durch zentrierte Differenzenannäherungen zweiter Ordnung für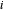 
von 1 bis 
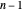darstellen.
Im Rand erlauben die Bedingungen der Nullableitung die Verwendung von fiktiven Punkten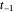 
und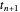 
. Wenn 
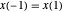und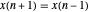 
, ist die Differenzformel zweiter Ordnung für die erste Ableitung 
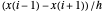null für 
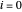und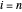 
. Verwenden Sie also am Rand Folgendes:
Die Trapezregel für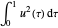 
wird wie folgt gegeben.
Da der Ausdruck der Trapezregel quadratisch ist und alle Beschränkungen lineare Gleichheitsbegrenzungen sind, kann das Minimum des diskretisierten Integrals direkt über QuadraticOptimization gefunden werden.
Näherungsfunktionen werden mit Interpolation gebildet.
Eine exakte analytische Lösung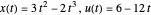 
ist für dieses Problem bekannt, daher ist es möglich, den Fehler in der Diskretisierung darzustellen.
Der asymptotische Fehler ist ungefähr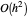 
, so dass durch Verdopplung von 
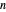auf 200 und Neuberechnung der Fehler etwa 1/4 dessen beträgt, was hier gezeigt wird.
Die analytische Lösung kann unter Berücksichtigung einer Familie von Kurven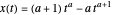 
gefunden werden, wobei 
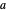ein Parameter ist. Diese parametrische Kurve erfüllt die vorgegebenen Randbedingungen 
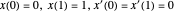. Da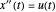 
, kann man einen optimalen Parameter 
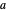finden, der 
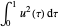minimiert.
Der optimale Wert von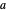 
ist bei 2. Dies ist auch das analytische Ergebnis von 
.
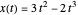