軌道最適化
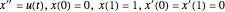 を条件として
を条件として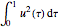 を最小化する.
を最小化する.
この例では,変分問題を,QuadraticOptimization等の凸法で効率的に解かれる有限最適化に離散化する方法を説明する.
変分問題は,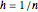 (
(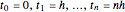 )のとき,区間[0,1]の均等間隔の格子上で積分するために,境界値問題を離散化して台形規則を使って近似される.
)のとき,区間[0,1]の均等間隔の格子上で積分するために,境界値問題を離散化して台形規則を使って近似される.
変数 u[i]が 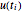 を, x[i]が
を, x[i]が 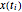 を表すとする.ここで
を表すとする.ここで 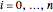 である.
である.
微分方程式の制約条件は,中央二次差分近似( は1から
は1から  )を使って簡単に表すことができる.
)を使って簡単に表すことができる.
境界では,ゼロの導関数条件により架空の点 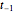 と
と 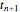 が使える.
が使える.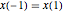 かつ
かつ 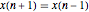 のとき,一次導関数
のとき,一次導関数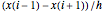 に対する二次差分公式は
に対する二次差分公式は 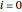 および
および 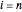 のときゼロになる.したがって,境界では以下が使える.
のときゼロになる.したがって,境界では以下が使える.
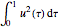 の台形公式は以下で与えられる.
の台形公式は以下で与えられる.
台形規則の式は二次式であり,制約条件はすべて線形等式制約なので,離散化された積分の最小値は直接QuadraticOptimizationを使って求めることができる.
近似関数はInterpolationを使って構築する.
この問題には厳密な解析解 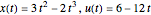 が知られているため,離散化の誤差をプロットすることができる.
が知られているため,離散化の誤差をプロットすることができる.
漸近誤差はほぼ 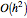 である.上の
である.上の  を2倍の200にして再計算すると,誤差はここで示されたものの約1/4になる.
を2倍の200にして再計算すると,誤差はここで示されたものの約1/4になる.
解析的解は,曲線 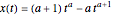 (
(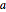 はパラメータ)の族を考えることで求めることができる. このパラメトリック曲線は所定の境界条件
はパラメータ)の族を考えることで求めることができる. このパラメトリック曲線は所定の境界条件 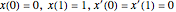 を満足する.
を満足する.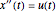 なので,
なので,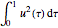 を最小化する最適パラメータ
を最小化する最適パラメータ 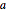 を求めることができる.
を求めることができる.
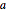 の最適の値は2におけるものであり,解析的結果は
の最適の値は2におけるものであり,解析的結果は 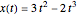 である.
である.