Dichte von Kugelpackungen berechnen
Der Entitätenbereich "Lattice" enthält nützliche Informationen über benannte Gittergraphen.
Betrachten Sie zum Beispiel den kubischen Gittergraphen, der einen Punkt in der Körpermitte und an allen Eckpunkten enthält (engl. BCC-Lattice), der über die Eigenschaft "Image" sofort visualisiert werden kann.
Eine wichtige Eigenschaft einer Kugelpackung ist der minimale verbleibende Leerraum im 3-dimensionalen Raum. Beim kubischen Gittergraphen wird die Dichte der Kugelpackung folgendermaßen angegeben.
Mit anderen Worten, Kugeln füllen etwa 68% des Gesamtraumes eines kubischen Raums.
Die minimalen Vektoren, die dieses Gitter erzeugen, stehen als Eigenschaft "MinimalVectors" zur Verfügung.
Vor diesem Hintergrund können Sie eine raumfüllende Visualisierung erstellen, aus der diese Dichte direkt berechnet werden kann. Beginnen Sie mit dem Erstellen einer Liste, die die Mittelpunkte der Kugeln enthält, die in der Einheitszelle aus den Minimalvektoren erscheinen.
Beschränken Sie nun den Darstellungsbereich auf den Bereich einer Einheitszelle.
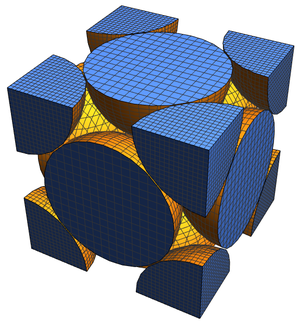
Die Visualisierung kann etwas aufwändiger gestaltet werden, indem gefüllte statt hohle Kugeln verwendet werden.
Wie aus diesem Diagramm ersichtlich ist, befinden sich acht Achtelkugeln und eine Vollkugel in der Einheitszelle, also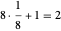 
Kugeln. Ausgehend von 
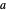als Kugelradius und vom Satz des Pythagoras, der auf eine Raumdiagonale angewendet wird, hat der Gesamtwürfel eine Kantenlänge 
, was bedeutet, dass die Packungsdichte der Kugeln durch den bereits gesehenen Ausdruck gegeben ist.
Betrachten Sie nun den kubischen Gittergraphen mit Punkten an den Außenseiten (engl. FCC-Lattice).
Diese Kubus hat eine höhere Packungsdichte.
Das heißt, Kugeln füllen daher etwa 74% des Gesamtraumes in dieser Kugelpackung.
Erstellen Sie wie vorhin eine raumfüllende Visualisierung, indem Sie zuerst die Mittelpunkte der Kugeln im Gittergraphen ermitteln.
Wie aus diesem Diagramm ersichtlich ist, befinden sich acht Achtelkugeln und sechs Halbkugeln in der Einheitszelle, also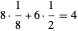 
ganze Kugeln. Mit 
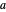als Kugelradius und ausgehend vom Satz des Pythagoras, der auf eine Seitendiagonale angewendet wird, hat der Gesamtwürfel eine Kantenlänge 
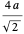, was bedeutet, dass die Packungsdichte der Kugeln durch den bereits erhaltenen Ausdruck gegeben ist.
Die hexagonal dichteste Kugelpackung (HCP) ist eine weiteres eng verwandtes Anordnungsproblem.
Sie hat dieselbe Packungsdichte wie die kubisch dichteste Kugelpackung (FCC).
Jede Kugel ist bei der hexagonal dichteste Kugelpackung von 12 weiteren Kugeln umgeben. Das Delaunay-Netz der Minimalvektoren für diese Packung enstpricht dem Verbinden der Mittelpunkte der äußeren 12 Kugeln und ermöglicht es, dass die Kanten die Flächen eines umschließenden Polyeders sind.
Daraus resultiert das Polyeder, das als dreieckige Orthobicupola bezeichnet wird.
