Fraktionale Knotenfärbung eines Graphen
Viele moderne Probleme – von Webseiten-Ranking über Schaltkreisentwürfe, Social Network-Analysen bis hin zu Absatzlogistik – können mit den Werkzeugen der Graphentheorie formuliert und gelöst werden. Zusätzlich zu einer großen Anzahl von Funktionen zum Erstellen, Rechnen mit und Arbeiten mit Graphen enthält die Wolfram Language eine Reihe von Graphensammlungen.
Der Entitätenbereich "Graph" versucht, interessante ungerichtete Diagramme zusammen mit so vielen ihrer Eigenschaften wie bekannt oder berechenbar zu katalogisieren. "Graph"-Entitäten bieten eine wachsende Sammlung von mehr als 6.000 Graphen und 500 vorberechneten Eigenschaften.
Die "Graph"-Entitäten bieten auch Einbettungen für die meisten Graphen.
Beachten Sie, dass die von der Eigenschaft "Graph" zurückgegebenen Objekte nicht nur Grafiken, sondern tatsächliche Wolfram Language-Graph-Objekte sind.
Jede Graphen-Entität enthält eine detaillierte Liste der mathematischen Klassen, zu denen sie gehört.
Es gibt auch zwei Funktionen, die die Welt der Grafik-Entitäten mit den Top-Level-Graphenobjekten verbinden. ToEntity konvertiert einen unbekannten einfachen Graph in eine Entität (falls eine existiert).
Den umgekehrten Vorgang führt FromEntity durch (was der Verwendung der Eigenschaft "Graph" entspricht).
Um sich ein Bild von der Breite der im Entitätenbereich "Graph" verfügbaren Daten zu machen, betrachten Sie die sogenannte chromatische Zahl oder Knotenfärbungszahl des Graphen. Die fraktionale Knotenfärbungszahl des Graphen ist anwendbar in Fällen, bei denen an jedem Knoten mehrere Farben mit jeweils einem bestimmten Gewichtungssanteil erlaubt sind, sodass je zwei beliebige benachbarte Knoten nicht dieselbe Farbe besitzen.
Während beispielsweise die chromatische Zahl des dodekaedrischen Graphens 3 ist (mindestens drei Farben sind erforderlich, um Knoten so einzufärben, dass keine zwei benachbarten Knoten eine Farbe teilen), ergibt die Verwendung der fraktionalen Knotenfärbungszahl eine fraktionale chromatische Zahl von 5/2 (von der Instanziierung, wie im nachstehend erläutert, aus fünf Farben besteht, die jedem Knoten mit Gewichtungen von 1/2 zugeordnet sind)
Die Graphen-Entitätsdomäne enthält sowohl die übliche und die fraktionale chromatische Zahl für viele Graphen, als auch konkrete Färbungen, die diese Minimalwerte erreichen. So hat beispielsweise der dodekaedrische Graph die chromatische Zahl 3.
Eine Färbung, die diesen Wert erreicht, kann wie folgt abgerufen werden.
Es ist ganz einfach, diese Einbettungs- und Färbungsdaten zusammen mit der integrierten Graphenfunktionalität zur Erstellung einer Visualisierung zu verwenden.
Wie visuell (oder programmgesteuert) verifiziert werden kann, haben im vorhergehenden Diagramm keine zwei benachbarten Knoten die gleiche Farbe.
Der Fall der fraktionierten Einfärbung ist etwas komplizierter, wobei jedoch die Enschränkung wegfällt, dass jeder Knoten eine einzige Farbe haben muss, sondern Knoten Bruch-Teile verschiedener Farben enthalten können. Die fraktionale chromatische Zahl wird definiert, indem die Brüche aller Knoten summiert werden. Dies ermöglicht oft eine Einfärbung mit "weniger" (wenn auch nicht unbedingt einer ganzen Zahl) Farben. Die frakionale chromatische Zahl des dodekaedrischen Graphen ist 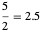 , was kleiner ist als die chromatische Zahl 3.
, was kleiner ist als die chromatische Zahl 3.
Um die fraktionierte Einfärbung zu erhalten, verwenden Sie die Eigenschaft "MinimumWeightFractionalColoring" um eine Liste von Knoten und Gewichtungen für verschiedene Farben zu erhalten.
Die vorhergehende Ausgabe zeigt beispielsweise an, dass eine minimale fraktionierte Einfärbung mit fünf Farben möglich ist, von denen die erste auf die Knoten 3, 5, 9, 12, 13, 15, 16 und 20 mit Gewicht 1/2 usw. angewendet wird. Da jede Farbe mit dem gleichen Gewicht von 1/2 aufgebracht wird, beträgt die gesamte chromatische Bruchzahl 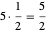 .
.
Da die Anteile jeder Färbung in diesem Fall gleich 1/2 sind, ist es einfach, eine Visualisierung zu erstellen, indem man zuerst die beiden Farben findet, die zu jedem Knoten beitragen.
Zum Beispiel zeigt die vorhergehende Liste an, dass der erste Knoten die Farben 4 und 5 verwendet, der zweite die Farben 4 und 5, der dritte die Farben 1 und 5 und so weiter. Konvertieren Sie nun numerische Farbindizes in richtige Farben.
Der letzte Schritt in der Visualisierung ist die Definition einer Knotenform-Funktion, die aus zwei entsprechend farbigen Halbkreisen besteht.
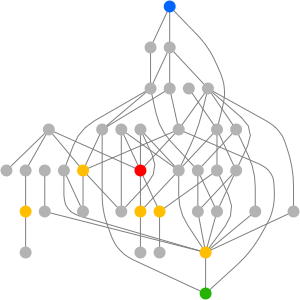
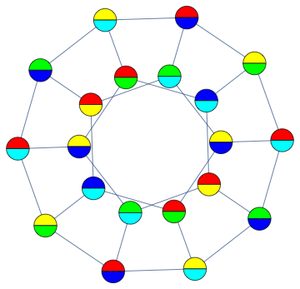
Jetzt können Sie eine minimale fraktionale Knotenfärbung für den dodekaedrischen Graphen erzeugen.
Wie erwartet, haben benachbarte Knoten keine gemeinsamen Farben in dieser fraktionalen Einfärbung.
Fraktionale chromatische Zahlen sind nicht gleichmäßig verteilt, sondern neigen dazu, sich um bestimmte Werte zu gruppieren. Die Erstellung eines Histogramms unter Verwendung der vorberechneten Daten für alle Graphen im Entitätenbereich "Graph" zeigt, dass sich Cluster um ganze Zahlen gruppieren, obwohl auch einige andere markante Spitzen sichtbar sind.
Sie können BubbleChart verwenden, um die Anzahl der Diagramme mit jeder fraktionalen chromatischen Zahl (mit Zähler und Nenner auf der 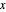 - und
- und 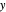 -Achse) darzustellen und die Verteilung genauer zu untersuchen.
-Achse) darzustellen und die Verteilung genauer zu untersuchen.