Kurven und ihre Eigenschaften in der Ebene visualisieren
Im Entitätenbereich "PlaneCurve" stehen viele ebene Kurven und eine große Anzahl vorberechneter Eigenschaften zur Verfügung.
So ist es beispielsweise einfach, geometrische Eigenschaften für parametrisierte Kurven abzurufen.
Hier werden formale Variablen (die als Buchstaben mit einem Punkt darunter wie in t geschrieben werden) verwendet, um Funktionsslots in Eigenschaften zu bezeichnen, die von Parametern abhängen. Die Werte bei einem bestimmten Parameter können dann einfach ersetzt werden, z.B. im Folgenden.
Auch die Visualisierung von Kurven und deren Eigenschaften ist einfach zu realisieren. Hier wird eine Rosettenkurve anhand ihrer Parametergleichungen gezeichnet und die Normale (grüner Pfeil) und Tangente (blauer Pfeil) an verschiedenen Punkten (roter Punkt) entlang der Kurve dargestellt.
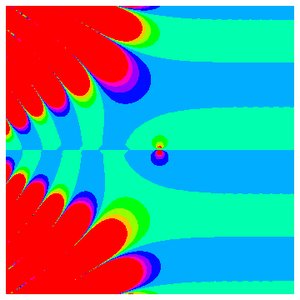
Ebenso kann man eine Kurve basierend auf einer bestimmten Eigenschaft, wie z.B. einer Krümmung, einfärben.
Hier werden die Bereiche mit der größten Krümmung blau, violett und rot hervorgehoben.
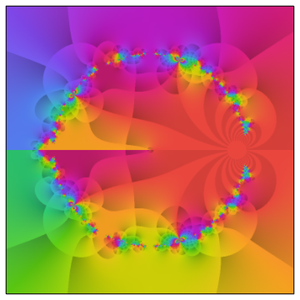
Eine noch farbenfrohere Visualisierung kann erreicht werden, wenn man mit der bekannten Kreisgleichung in kartesischen Koordinaten beginnt.
Extrahieren Sie den von den Koordinatenpositionen abhängigen Teil der Gleichung und nehmen Sie dann den Radius als Skalierungskonstante, um ebene Kurven mit der Form eines Kreises zu konstruieren.
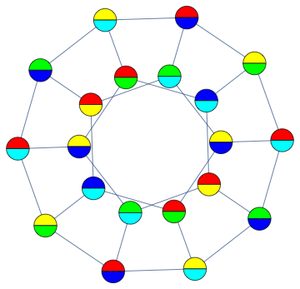
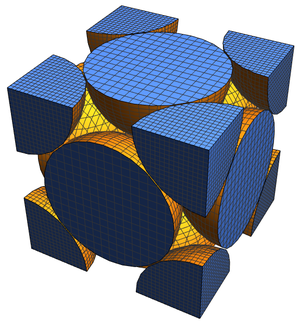
Die Grenzen (Boundaries) eines gefüllten Quadrats können ebenfalls als kartesische Gleichung ausgedrückt werden.
Solche Darstellungen sind im Entitätenbereich "PlaneCurve" für Vielecke bis hin zum Fünfeck verfügbar.
Der Prozess der Konstruktion solcher Darstellungen kann verallgemeinert werden, um polygonale Pegelkurven in jedem gewünschten Grad zu erzeugen.