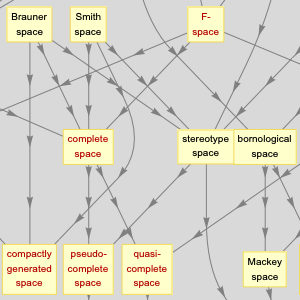
Funktionenräume untersuchen
Ein Funktionenraum ist eine Menge von Funktionen, die alle denselben Definitionsbereich von Menge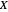 
bis Menge 
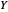besitzen. Er wird als Raum bezeichnet, weil er in vielen Anwendungen ein topologischer Raum ist und oft mit einem Messraum verbunden ist.
Funktionsräume neigen dazu, topologische Konzepte zu verwenden, die sehr allgemein und abstrakt sind. Der Entitätenbereich "FunctionSpace" umfasst Eigenschaften von mehr als 125 Räumen, die für Berechnungen geeignet sind.
Lebesgue-Räume werden beispielsweise durch eine natürliche Verallgemeinerung der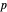 
-fach integrierbaren Funktionen für endliche Vektorräume definiert. Eine schöne Zusammenfassung der Eigenschaften des 
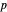Lebesgue-Raums in 
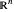kann direkt aus einer Wolfram|Alpha-Abfrage bezogen werden, die hier so angepasst wurde, um nur die wichtigsten Pods anzuzeigen.
Lebesgue-Räume können unterschiedlicher Art definiert sein, je nach ihrem Definitionsbereich und Maßraum.
Sehen Sie sich nun den Sonderfall des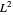 
-Raums an, dessen Norm wie folgt definiert ist.
Hier wird der PureMath-Kontext als Platzhalter für mathematische Objekte verwendet, die (noch?) nicht in die Wolfram Language eingebaut sind.
Informationen über Mathematiker, die bestimmte Räume untersucht haben, stehen ebenfalls zur Verfügung.
Der Einfachheit halber ist auch eine tabellarische Darstellung der verschiedenen verwendeten Notationen für jeden Raum möglich.
Als Beispiel dafür, wie die Informationen in diesem Entitätenbereich verwendet werden können, werden einige einfache Berechnungen durchgeführt.
Sehen Sie sich den Dualraum von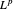 
(für 
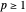) an.
Nehmen Sie nun das Dual des Dualraums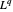 
und führen Sie eine symbolische Vereinfachung der resultierenden parametrisierten Entität durch.
Da dies gleich dem ursprünglichen Raum ist, können Sie sehen, dass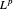 
reflexiv ist, d.h. 
.
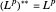Dies kann auch direkt berechnet werden.
Detailliertere Informationen über Leerzeichen erhalten Sie über die Eigenschaft "TypesetDescription", die im Fall eines reflexiven Raums die folgende strenge Definition zusammen mit einer hilfreichen zusätzlichen Beschreibung liefert.
