Die Riemannsche Hypothese untersuchen
Die Riemannsche Hypothese, die erstmals in einem bahnbrechenden Artikel von Bernhard Riemann aus dem Jahr 1859 veröffentlicht wurde, ist eine mathematische Annahme, die besagt, dass die nicht-trivialen Nullstellen der Riemann-Zeta-Funktion d.h. die Werte der Riemann-Zetafunktion
außer 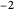 ,
, 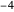 ,
, 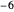 , … sodass
, … sodass 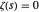 alle auf der "kritischen Geraden"
alle auf der "kritischen Geraden" 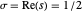 liegen, wobei
liegen, wobei 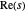 der Realteil einer komplexen Variablen
der Realteil einer komplexen Variablen 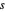 ist.
ist.
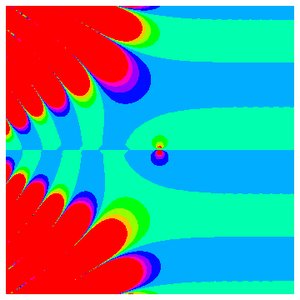
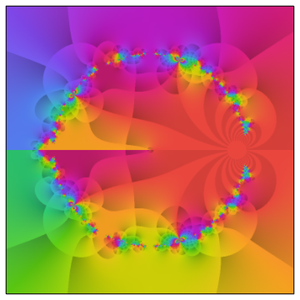
Während die Riemann-Zeta-Funktion unendlich entlang der negativen Realachse osziliiert, nähert sie sich asymptotisch der 1 entlang der positiven Realachse.
Das Verhalten wird entlang der kritischen Linie noch komplizierter.
Tatsächlich gibt die vorhergehende Handlung eine repräsentativere Vorstellung von der wahren Komplexität, die in der komplexen Ebene entsteht.
Die ersten 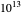 nicht-trivialen Nullstellen der Riemann-Zetafunktion wurden getestet und erfüllen die Riemannsche Hypothese. Es ist daher ziemlich überraschend, dass trotz so zahlreicher numerischer Beweise und trotz erheblicher Anstrengungen niemand in den letzten 250 Jahren die Hypothese beweisen konnte.
nicht-trivialen Nullstellen der Riemann-Zetafunktion wurden getestet und erfüllen die Riemannsche Hypothese. Es ist daher ziemlich überraschend, dass trotz so zahlreicher numerischer Beweise und trotz erheblicher Anstrengungen niemand in den letzten 250 Jahren die Hypothese beweisen konnte.
Viele Ergebnisse der Mathematik sind bekannt "unter der Annahme, dass die Riemannsche Hypothese gilt". Das bedeutet, dass ein Nachweis der Riemannschen Hypothese sofort eine Vielzahl weiterer Ergebnisse in der Mathematik erbringen würde. Es gibt auch viele alternative Formulierungen der Riemannschen Hypothese, eine Sammlung, die der Entitätenbereich RiemannHypothesisFormulation zusammenzustellen zu versucht.
Die Sammlung umfasst derzeit insgesamt rund 70 Formulierungen.
Diese Formulierungen können wiederum zu etwa halb so viele Familien zusammengefasst werden.
Die ursprüngliche Form der Riemannschen Hypothese kann mit Hilfe der Quantorarithmetik in der folgenden prägnanten Form angegeben werden.
Während dies im Prinzip ein berechenbarer Ausdruck ist, kann die Anwendung eines Quantors auf die Hypothese nicht ausgewertet werden, da die Riemannsche Hypothese bislang nicht bewiesen ist (schließlich wäre Mathematica in diesem Fall in der Lage, die Gültigkeit der Riemannschen Hypothese festzustellen, wenn Mathematica die Quantoren auflösen könnte).
Untersuchen Sie nun die Arten von alternativen Formulierungen, die im Bereich RiemannHypothesisFormulation zur Verfügung stehen.
Die vielleicht berühmteste alternative Aussage der Riemannschen Hypothese betrifft die Positivität von Ausdrücken, die von Derivaten der 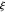 -Funktion gegeben werden– einer Funktion, die eng mit
-Funktion gegeben werden– einer Funktion, die eng mit 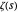 verbunden ist. Diese Formulierung, bekannt als Li-Ungleichung, kann wie folgt formell formuliert werden.
verbunden ist. Diese Formulierung, bekannt als Li-Ungleichung, kann wie folgt formell formuliert werden.
Die Wolfram Language kann direkt geschlossene Formen für den Ausdruck innerhalb der Ungleichung berechnen (obwohl dies für große Indizes die Verwendung bekannter Wiederholungsbeziehungen erfordert, die durch die Ableitungen von 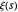 erfüllt werden). Extrahieren Sie zunächst die Ungleichung aus der Formulierung.
erfüllt werden). Extrahieren Sie zunächst die Ungleichung aus der Formulierung.
Definieren Sie nun die Li-Konstanten 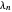 deren Positivität für alle positiven
deren Positivität für alle positiven 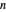 der Riemannschen Hypothese entspricht.
der Riemannschen Hypothese entspricht.
Das genaue Berechnen und Numerieren der Konstanten bis zur Ordnung fünf bestätigt, dass sie tatsächlich positiv sind.
Natürlich ist die Li-Ungleichung nur eine alternative Formulierung. Eine Reihe von Mathematikern haben mehrere Formulierungen für die Riemann-Hypothese abgeleitet. Hier ist eine Liste von Mathematikern, die eine Vermutung formuliert haben, geordnet nach der Anzahl der verschiedenen Formulierungen, die in der Sammlung enthalten sind.
Sie können nun eine Zeitleiste von Mathematikern erstellen, die sich mit der Riemannschen Hypothese befasst haben, um die hohe Aktivität veranschaulicht, die Riemanns schöner, aber komplexer Hypothese gewidmet ist.