Calculez les densités des empilements en treillis
Le domaine d'entités "Lattice" contient des informations utiles sur les treillis dits "classiques".
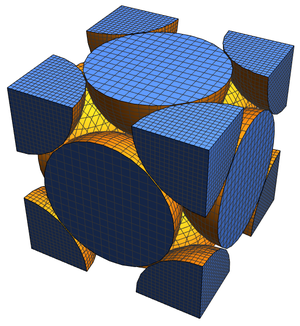
Prenons par exemple le réseau cubique centré sur le corps (BCC), qui peut être immédiatement visualisé en utilisant la propriété "Image".
Une propriété importante d'un empilement en treillis est la fraction d'espace occupée par les sphères empilées avec la configuration correspondante. Pour un treillis BCC, cette densité d'empilement est donnée par ce qui suit.
En d'autres termes, les sphères occupent environ 68 % de l'espace total dans un empilement cubique centré sur le corps.
Les vecteurs minimaux générant ce treillis sont disponibles sous la propriété "MinimalVectors".
À partir de ces données, vous pouvez réaliser une visualisation de remplissage d'espace à partir de laquelle cette densité peut être directement calculée. Commencez par construire une liste donnant les centres des sphères apparaissant dans la cellule unitaire à partir des vecteurs minimaux.
Limitez maintenant la portée de la représentation graphique à la région de la cellule unitaire.
La visualisation peut être légèrement plus élaborée en utilisant des boules remplies au lieu de boules creuses.
Comme on peut le voir sur ce diagramme, il y a huit huitièmes de sphère et une sphère pleine dans la cellule unitaire, ce qui représente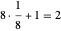 
sphères pleines. En prenant 
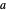comme rayon des sphères, par le théorème de Pythagore appliqué à une diagonale d'espace, la longueur des arêtes du cube global est 
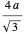, c'est-à-dire que la densité de remplissage des sphères est donnée par l'expression qui a déjà été vue.
Considérons maintenant le treillis cubique centré sur la face (FCC en anglais).
Cet empilement en treillis a une densité d'empilement plus élevée.
C'est-à-dire que les sphères occupent environ 74 % de l'espace total dans un empilement cubique à faces centrées.
Comme précédemment, effectuez une visualisation de remplissage d'espace en trouvant d'abord les centres des sphères dans un empilement FCC.
Comme on peut le voir sur ce diagramme, il y a huit huitièmes et six demi-sphères dans la cellule unitaire, ce qui représente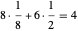 
sphères complètes. En prenant 
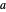comme rayon des sphères, par le théorème de Pythagore appliqué à une diagonale de face, la longueur des arêtes du cube global est 
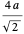, c'est-à-dire que la densité de remplissage des sphères est donnée par l'expression déjà extraite.
L'empilement hexagonal fermé (HCP) est un autre empilement étroitement lié.
Il a la même densité d'empilement que le cubique à faces centrées.
Comme dans l'empilement cubique à faces centrées, chaque sphère est entourée de 12 autres sphères dans HCP. En prenant le maillage Delaunay des vecteurs minimaux de cet empilement, cela équivaut à relier les centres des 12 sphères externes et permettre aux arêtes de constituer les faces d'un polyèdre fermé.
Il en résulte le polyèdre connu sous le nom d'orthobicupule triangulaire.
