Visualisez les identités de fractions continues
Le type d'entités "ContinuedFraction" contient des milliers d'identités de fractions continues ainsi que de nombreuses propriétés associées pré-calculées.
Par exemple, il est facile de récupérer une classe d'entités constituée d'identités de fractions continues connues pour la fonction cosinus.
Vous pouvez obtenir une liste explicite d'entités pour le cosinus avec EntityList.
Vous pouvez également visualiser les identités explicitement.
Choisissez maintenant les identités où le côté gauche est explicitement Cos[z] (sans facteur d'échelle supplémentaire dans l'argument).
Calculez les convergences paires finies des ordres 2 à 12 et visualisez comment les convergences suivantes deviennent de meilleures approximations de la fonction cosinus.
Explorez maintenant un certain nombre d'identités de fractions continues plus compliquées (et plus attrayantes). Un certain nombre d'entre elles sont associées à Ramanujan.
Ces identités impliquent les fonctions mathématiques connues sous le nom de fonctions thêta de Jacobi et les symboles de Pochhammer.
La dernière d'entre elles (la fraction continue de Rogers-Ramanujan) est une identité particulièrement séduisante définie par les puissances d'imbrication d'une variable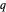 
.
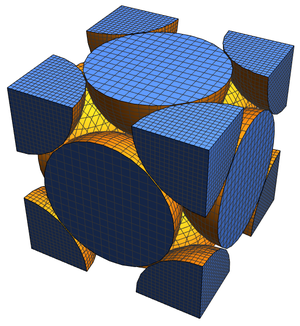
Bien que sa définition soit simple, la fraction continue de Rogers-Ramanujan a une structure très riche dans le plan complexe. Pour visualiser ceci, affichez la structure complexe des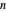 
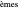convergents en représentant graphiquement la partie réelle, la partie imaginaire et le module pour 
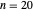sous forme de tracés de contour.
Une vue légèrement différente peut être obtenue avec des représentations graphiques en 3D.
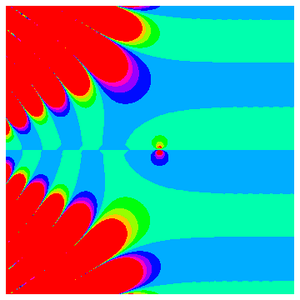
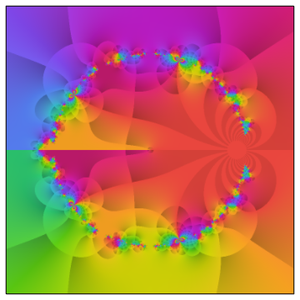
Pour conclure l'exploration visuelle de la fonction Rogers-Ramanujan, utilisez ComplexPlot pour obtenir une vue détaillée de certaines de ses structures complexes en représentant graphiquement l'argument complexe de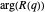 
avec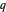 
variant dans le plan complexe.
