Explorez les relations de groupe et les générateurs
Le domaine d'entités "FiniteGroup" répertorie les données détaillées sur les groupes notables d'ordre fini.
La liste des groupes comprend les 23 groupes sporadiques, dont le plus important est le groupe Monster et dont les premiers sont présentés ici avec leur ordre de groupe.
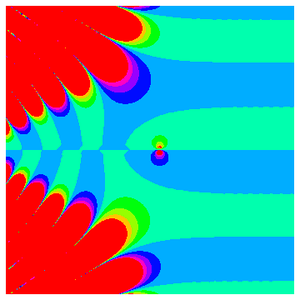
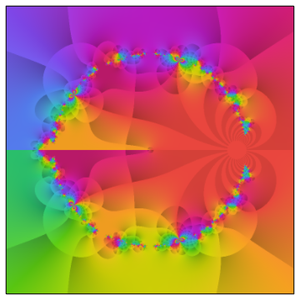
Un certain nombre de visualisations intéressantes peuvent être faites à partir de groupes finis. Avec ArrayPlot une simple représentation graphique de la table de multiplication permet de visualiser la structure des bandes et des blocs dans les représentations sous-jacentes.
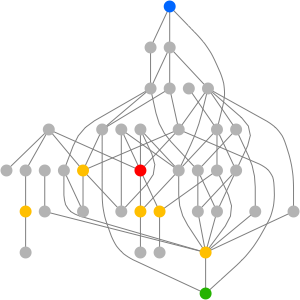
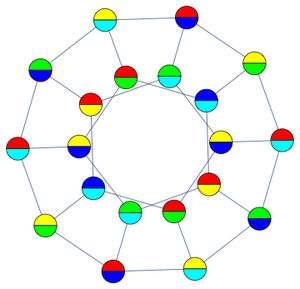
Le graphe de Cayley est une autre façon de visualiser les groupes. Le graphe de Cayley, associé à un graphe donné et à la partie génératrice, est défini comme le graphe dirigé ayant un sommet associé à chaque élément de groupe et des arêtes dirigées 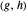 lorsque
lorsque 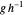 est un élément d'une partie génératrice. (Le graphe de Cayley peut dépendre du choix d'une partie génératrice.)
est un élément d'une partie génératrice. (Le graphe de Cayley peut dépendre du choix d'une partie génératrice.)
Par exemple, le graphe de Cayley du groupe abélien 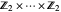 est donné par le graphe hypercube bidirectionnel
est donné par le graphe hypercube bidirectionnel 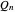 .
.
La correspondance avec le graphe hypercube peut être vérifiée en utilisant ToEntity, qui renvoie les entités correspondantes de l'hypercube "Graph".
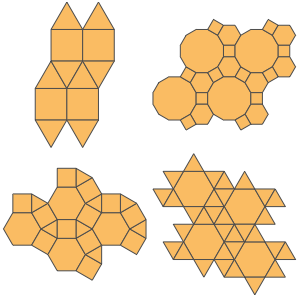
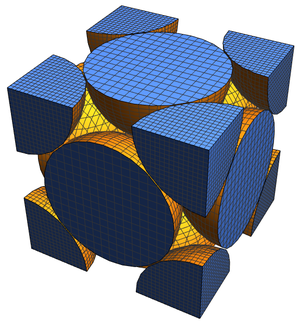
Les graphes de Cayley des groupes de points cristallographiques tétraédriques correspondent à des graphes nommés dérivés des squelettes de polyèdres semi-réguliers (archimédiens).
Là encore, les graphes associés peuvent être obtenus par programmation.
Ceux-ci peuvent à leur tour être convertis en entités du domaine d'entités "Polyhedron" qui possèdent des squelettes correspondant à ces graphes.