Explorez les espaces de fonctions
Un espace de fonctions est un ensemble de fonctions d'un type donné, d'un ensemble 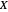 à un autre ensemble
à un autre ensemble 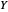 . On l'appelle un espace parce que dans de nombreuses applications, c'est un espace topologique qui est souvent associé à un espace de mesure.
. On l'appelle un espace parce que dans de nombreuses applications, c'est un espace topologique qui est souvent associé à un espace de mesure.
Les espaces de fonctions tendent à impliquer des concepts topologiques très généraux et abstraits. Le domaine d'entités "FunctionSpace" encode les propriétés de plus de 125 espaces et les rend disponibles dans un format adapté aux calculs.
Par exemple, les espaces de Lebesgue sont définis en utilisant une généralisation naturelle de la norme 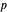 pour les espaces vectoriels de dimension finie. Un récapitulatif des propriétés de l'espace de Lebesgue d'ordre
pour les espaces vectoriels de dimension finie. Un récapitulatif des propriétés de l'espace de Lebesgue d'ordre 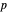 sur
sur 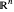 peut être obtenu directement à partir d'une requête Wolfram|Alpha, qui est ici personnalisée pour afficher uniquement les modules les plus significatifs.
peut être obtenu directement à partir d'une requête Wolfram|Alpha, qui est ici personnalisée pour afficher uniquement les modules les plus significatifs.
Il existe en fait de nombreuses variétés d'espaces de Lebesgue définis, en fonction de leur domaine et de l'espace de mesure.
Considérons maintenant le cas particulier de l'espace 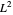 , avec la norme définie comme suit.
, avec la norme définie comme suit.
Ici, le contexte PureMath est utilisé comme espace réservé pour les objets mathématiques qui ne sont pas (encore ?) intégrés dans Wolfram Language.
Des informations sur les personnes notables ayant étudié chaque espace sont également disponibles.
Pour plus de commodité, un tableau indiquant les différentes notations utilisées pour chaque espace est également fourni.
Quelques calculs simples sont effectués pour illustrer la façon dont l'information dans ce domaine d'entités peut être utilisée.
Considérons l'espace dual de 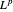 (pour
(pour 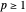 ).
).
Prenons maintenant le dual de l'espace dual 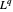 et effectuons une simplification symbolique sur l'entité paramétrée qui en résulte.
et effectuons une simplification symbolique sur l'entité paramétrée qui en résulte.
Puisqu'il est égal à l'espace d'origine, vous pouvez voir que 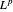 est réflexif, c'est à dire que
est réflexif, c'est à dire que 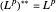 .
.
Ceci peut aussi être calculé directement.
Des informations plus détaillées sur les espaces sont fournies via la propriété "TypesetDescription" qui, dans le cas d'un espace réflexif, donne la définition rigoureuse suivante ainsi qu'une description complémentaire utile.