Wolfram Language™

Étudiez l'hypothèse de Riemann

Publiée pour la première fois en 1859 par Bernhard Riemann dans un article révolutionnaire, l'hypothèse de Riemann est une conjecture mathématique profonde qui stipule que les zéros non triviaux de la fonction zêta de Riemann, c'est-à-dire les valeurs de la fonction zêta de Riemann

sauf 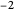, , 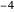, 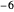… de sorte que 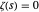, se situent toutes sur la "ligne critique" 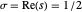, où 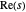représente la partie réelle de la variable complexe .

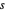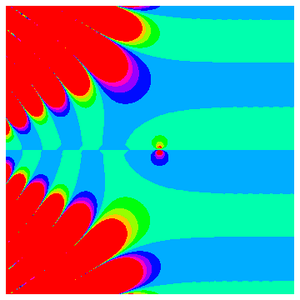
Alors que la fonction zêta de Riemann oscille à l'infini le long de l'axe réel négatif, elle se rapproche asymptotiquement de 1 le long de l'axe réel positif.

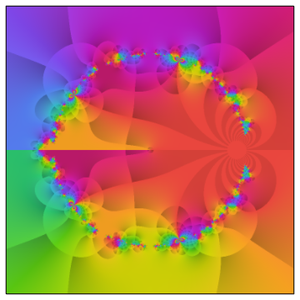
Le comportement devient encore plus compliqué le long de la ligne critique.

En fait, le graphique précédent donne une idée plus représentative de la véritable complexité qui se présente dans le plan complexe.

Les 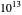premiers zéros non triviaux de la fonction zêta de Riemann ont été testés et répondent à l'hypothèse de Riemann. Il est donc assez surprenant que, en dépit d'une telle abondance de preuves numériques et d'efforts considérables, personne n'ait été en mesure de prouver cette hypothèse au cours des 250 dernières années.

De nombreux résultats en mathématiques sont connus "en supposant que l'hypothèse de Riemann tient la route". Cela signifie qu'une preuve de l'hypothèse de Riemann établirait immédiatement une multitude d'autres résultats en mathématiques. Il existe également de nombreuses formulations alternatives de l'hypothèse de Riemann, une collection que le domaine d'entités RiemannHypothesisFormulation tente de rassembler.

La collection contient actuellement un total d'environ 70 formulations.

Ces formulations peuvent à leur tour être regroupées dans environ la moitié de ces familles.

La forme originale de l'hypothèse de Riemann peut être énoncée en utilisant l'arithmétique de quantificateur dans la forme concise suivante.

Bien qu'il s'agisse en principe d'une expression calculable, puisque personne ne sait comment établir l'hypothèse de Riemann, l'application d'un quantificateur à l'hypothèse ne peut pas être évaluée car l'hypothèse de Riemann n'a pas encore été prouvée (après tout, si Mathematica pouvait résoudre les quantificateurs dans le cas présent, il serait capable de déterminer la validité de l'hypothèse de Riemann).

Examinons maintenant les types de formulations alternatives présentes dans le domaine RiemannHypothesisFormulation.

L'affirmation alternative la plus célèbre de l'hypothèse de Riemann concerne la positivité des expressions données par les dérivées de la fonction 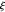(une fonction étroitement liée à 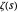) est sans doute l'inégalité de Li. Cette formulation, connue sous le nom d'inégalité de Li, peut être formellement énoncée comme suit.

Wolfram Language peut calculer directement des formes fermées pour l'expression à l'intérieur de l'inégalité (bien que cela nécessite, pour les grands indices, l'utilisation de relations de récurrence connues satisfaites par les dérivées de 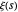). Pour commencer, il faut d'abord extraire l'inégalité de la formulation.

Définissez maintenant les constantes 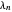de Li dont la positivité pour tous les 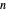positifs est équivalente à l'hypothèse de Riemann.

En calculant exactement et en numérotant les constantes jusqu'à cinq, on vérifie qu'elles sont effectivement positives.

Bien sûr, l'inégalité de Li n'est qu'une formulation alternative. Un certain nombre de mathématiciens ont dérivé des formulations multiples pour l'hypothèse de Riemann. Voici une liste de mathématiciens classés selon le nombre de formulations distinctes représentées dans la collection.

Vous pouvez maintenant établir une chronologie des chercheurs qui illustre dans une certaine mesure le niveau élevé d'activité qui a été consacré à la belle mais complexe hypothèse de Riemann.