Les conteneurs les plus efficaces pour une forme donnée
Le domaine d'entités "Solid" contient des régions fermées dans l'espace qui présentent un intérêt mathématique.
De nombreuses propriétés sont disponibles pour chaque solide.
Naturellement, deux de ces propriétés sont la superficie et le volume.
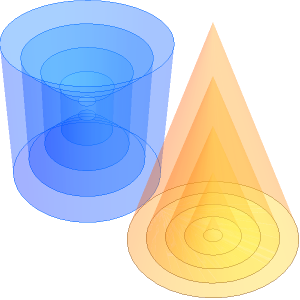
Comme on le sait, le rapport superficie/volume de toutes les formes possibles est minimisé par la sphère remplie (boule). Cependant, il est également intéressant de prendre en compte les paramètres qui minimisent la superficie nécessaire pour inclure un volume fixe pour d'autres familles de solides. Par exemple, il est facile de montrer que le cylindre plein qui optimise le plus efficacement son volume a un rapport hauteur/rayon de base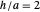 
(ou l'équivalent, un diamètre de base égal à sa hauteur).
Vous pouvez aussi considérer d'autres solides, où pour des raisons de simplicité, le volume est fixé à l'unité.
De tous les cuboïdes, le cube (c'est-à-dire le cuboïde équilatéral) fournit le plus grand volume contenu par superficie.
Un tétraèdre tri-rectangulaire a également la plus petite superficie pour un volume donné si ses arêtes ont les mêmes longueurs le long des axes cartésiens.
Pour un cône plein, les dimensions qui minimisent la superficie peuvent également être calculées sous forme fermée.
Vous pouvez maintenant visualiser les solides les plus efficaces pour ces formes car les dimensions globales sont variées.
