격자 충전의 밀도 계산하기
"Lattice" 실체 영역은 고전적인 이름이 붙은 격자에 대한 유익한 정보를 담고 있습니다.
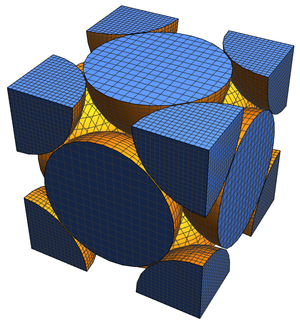
예를 들어 "Image" 특성을 사용해 즉시 시각화할 수 있는 체심 입방(BCC) 격자에 대해 생각해 봅니다.
격자충전의 중요한 특성은 적절한 배치로 충전된 공에 의해 차지되는 공간의 비율입니다. 체심 입방 격자의 경우 이 충전 밀도는 아래와 같이 주어집니다.
즉, 공은 체심 입방 충전 공간 전체의 약 68 퍼센트를 차지합니다.
이 격자를 생성하는 최소 벡터는 "MinimalVectors" 특성으로 사용할 수 있습니다.
이것을 이용해 공간 채우기 시각화를 작성할 수 있고, 거기에서 직접 밀도를 계산할 수 있습니다. 단위 격자 내에 나타나는 공의 중심을 주는 목록을 최소 벡터에서 구축하는 것부터 시작합니다.
다음으로 플롯 범위를 단위 격자의 영역으로 제한합니다.
속이 빈 구체 대신 채워진 구를 사용하여 보다 정교하게 시각화할 수 있습니다.
이 그림을 통해 알 수 있듯이, 단위 격자 중에는 8분의 1의 공 8개와 전체 공이 1개, 그러므로 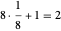 개의 완전한 공이 있는 것입니다. 공의 반지름을
개의 완전한 공이 있는 것입니다. 공의 반지름을 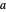 로 하면 피타고라스의 정리를 공간 대각선에 적용하여, 입방체 전체 변의 길이는
로 하면 피타고라스의 정리를 공간 대각선에 적용하여, 입방체 전체 변의 길이는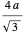 이 됩니다. 이는 공의 충전 밀도가 이미 식에 표시된 표현에 의해 주어진다는 것을 의미합니다.
이 됩니다. 이는 공의 충전 밀도가 이미 식에 표시된 표현에 의해 주어진다는 것을 의미합니다.
이제 면심 입방(FCC) 격자에 대해 알아봅니다.
이 격자 충전은 충전의 밀도가 더 높습니다.
즉, 공이 면심 입방 격자 충전의 전체 공간의 약 74 퍼센트를 차지합니다.
이전과 마찬가지로 면심 입방 격자 충전의 구심점을 찾음으로써 공간 충전의 시각화를 작성합니다.
이 그림에서 볼 수 있듯이, 단위 격자 안에는 8분의 1의 공 8개와 절반의 공 6개 있으며 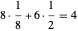 개의 완전한 공이 있는 것입니다. 공의 반지름을
개의 완전한 공이 있는 것입니다. 공의 반지름을 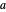 로 하면 피타고라스의 정리를 면의 대각선에 적용하여, 입방체 전체 변의 길이는
로 하면 피타고라스의 정리를 면의 대각선에 적용하여, 입방체 전체 변의 길이는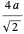 이 됩니다. 이는 공의 충전 밀도가 이미 표시된 표현에 의해 주어진다는 것을 의미합니다.
이 됩니다. 이는 공의 충전 밀도가 이미 표시된 표현에 의해 주어진다는 것을 의미합니다.
조밀 육방 격자(HCP) 또한 밀접하게 관련된 충전입니다.
이 충전의 밀도는 면심 입방 격자와 같습니다.
면심 입방 격자의 최밀 충전에서와 같이 조밀 육방 충전은 각각의 공이 12개의 다른 공으로 둘러싸여 있습니다. 이 충전을 위해 최소 벡터의 델로네(Delaunay) 메시를 취하는 것은, 외부 12개의 공의 중심을 연결하고 그 가장자리를 둘러싸는 다면체의 면이 되도록 하는 것과 같습니다.
이것은 결과적으로, 맞붙인 두 삼각지붕(triangular orthobicupola)으로 알려진 다면체가 됩니다.