그래프의 분수 채색하기
웹페이지의 순위, 전자회로의 설계, 소셜 네트워크의 분석, 유통 관리 등 폭넓은 분야를 아우르는 현대 사회의 문제는 대부분 그래프 이론의 도구를 사용하여 공식화되어 해결할 수 있습니다. 그래프의 구축이나 조작과 그래프를 사용한 계산을 위한 많은 함수와 더불어 Wolfram 언어에는 다수의 그래프가 포함되어 있습니다.
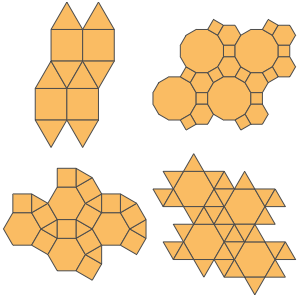
"Graph" 실체 영역은 흥미로운 무향 그래프를 되도록 많은 기존의 알려진 혹은 계산 가능한 특성과 함께 분류하는 것을 목표로 하고 있습니다. "Graph" 실체는 600개 이상의 간단한 그래프와 500개 이상의 사전 계산된 특성을 제공하고 있으며, 이 숫자는 지속적으로 증가하고 있습니다.
"Graph" 실체의 프레임워크에는 대부분의 그래프의 사전 계산된 "멋진" 매립도 포함되어 있습니다.
"Graph" 특성이 반환하는 객체는 단순한 그래프가 아닌 Wolfram 언어의 실제 Graph 객체라는 점에 유의해야 합니다.
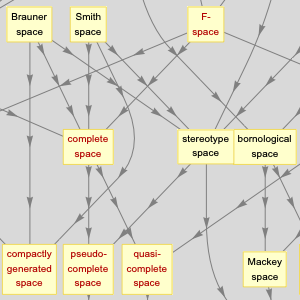
각 그래프의 실체는 그 그래프가 속한 수학 클래스의 상세 목록을 포함합니다.
또한 그래프 실체와 최상위 그래프 객체를 잇는 두 개의 함수도 있습니다. ToEntity는 미지의 간단한 그래프를 실체(존재한다면)로 변환합니다.
그 반대는 FromEntity에 의해 주어지는데 이는 "Graph" 특성을 사용하는 것과 같습니다.
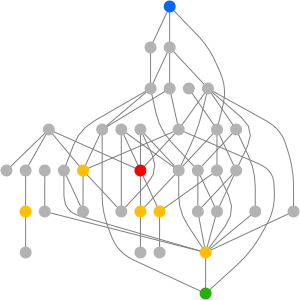
"Graph" 실체 영역에서 이용 가능한 데이터의 확산을 알기 위해, 이른바 그래프의 분수 채색 수를 생각해 봅니다. 분수 채색 수는 일반적인 채색 수를 채색에 대해 일반화한 것입니다. 여기서 정점은 각각이 지정된 무게 비율을 가지며, 인접하는 정점이 같은 색이 되지 않도록 각각 다른 색으로 채색됩니다.
예를 들어, 12면체 그래프의 채색 수는 3색(인접한 두 정점이 같은 색이 되지 않도록 다른 색으로 칠하기 위해서는 최소 3가지 색이 필요)이지만, 분수 채색을 사용하면, 5/2라는 분수의 채색 수가 주어집니다. 나중에 설명하는 인스턴스화 중 하나로, 5개의 색이 1/2 무게로 각 노드에 할당됩니다.
그래프 실체 영역은 여러 그래프에 대해서 일반적인 채색 수와 분수 채색 수를 모두 이러한 최소값을 달성하는 구체적인 채색과 함께 포함합니다. 예를 들어 12면체 그래프의 채색 수는 3입니다.
이 값을 실현하는 채색은 다음과 같이 추출할 수 있습니다.
이 매립과 채색 데이터를 임베디드 그래프 기능과 함께 사용하여 매우 간단하게 시각화를 작성할 수 있습니다.
위의 그림을 통해(혹은 프로그램을 사용하여) 확인할 수 있듯이 같은 색의 인접 정점은 존재하지 않습니다.
분수 채색은 좀 더 복잡하지만, 기본적으로 정점이 다른 색을 분수 비율로 포함하는 것을 허용함으로써 각 정점이 고유한 색을 가진다는 제약 조건이 완화됩니다. 분수 채색 수는 모든 정점에 대해서 분수 비율을 합계하여 정의되어 종종 "더 적은" 색(반드시 정수는 아니지만)의 채색이 가능합니다. 예를 들어 12면체 그래프의 분수 채색 수는 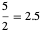 이고, 일반적인 채색 수의 3보다 적습니다.
이고, 일반적인 채색 수의 3보다 적습니다.
분수채색을 얻기 위해서는 "MinimumWeightFractionalColoring" 특성을 사용하여 정점과 다른 색의 무게 목록을 얻습니다.
예를 들어 위의 출력은 최소 분수 채색은 5색을 사용하면 가능하며, 최초의 색이 정점 3, 5, 9, 12, 13, 15, 16, 20에 무게 1/2로 적용되는 것을 의미합니다. 각 색상이 1/2이라는 똑같은 무게로 적용되므로, 전체적인 분수 채색 수는 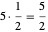 가 됩니다.
가 됩니다.
이 경우는 각 색상의 비율이 1/2에 동일하므로, 시각화는 쉽게 구할 수 있습니다. 우선, 각 정점의 두 색을 구합니다.
예를 들어, 위의 목록은 첫 번째 정점이 색 4와 색 5, 그리고 두 번째 정점 또한 색 4와 색 5를 사용하며, 세 번째 정점은 색 1과 색 5를 사용함을 나타납니다. 이제 숫자 색상 인덱스를 실제 색으로 변환합니다.
시각화의 마지막 단계는 적절하게 채색된 두 개의 반원으로 구성된 정점 모양의 함수를 정의하는 것입니다.
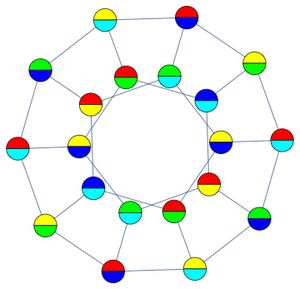
모든 것이 갖추어지면 12면체 그래프의 최소 분수 채색을 표시할 수 있습니다.
예상대로, 이 분수의 채색은 같은 색의 인접 정점이 없습니다.
분수 채색 수는 균일하게 분포되어 있지는 않지만 특정 값으로 모이는 경향이 있습니다. "Graph" 실체 영역의 전체 그래프에 대한 사전 계산된 데이터의 히스토그램을 만들면 그 밖에도 집중되어 있는 값은 있으나 값이 정수 주위에 모여 있음을 알 수 있습니다.
BubbleChart를 사용하면 각 분수 채색 수를 가진 그래프의 수를 (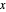 축에 분자,
축에 분자, 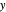 축에 분모를 사용) 플롯하여 분포를 보다 자세히 알아볼 수 있습니다.
축에 분모를 사용) 플롯하여 분포를 보다 자세히 알아볼 수 있습니다.