주어진 형태에 대한 가장 효율적인 컨테이너
"Solid" 실체 영역에는 수학적으로 흥미로운 공간의 닫힌 영역이 포함되어 있습니다.
각각의 입체에 대하여 다수의 특성을 이용할 수 있습니다.
당연히 이러한 특성 중 두 개는 표면적과 부피입니다.
잘 알려진 것처럼, 부피에 대한 표면적의 비율은 모든 모양에서 채워진 구(공)의 형상으로 최소화됩니다. 그러나, 다른 고형군의 입체에 대해서 일정한 부피를 둘러싸는 데 필요한 표면적을 최소화하는 파라미터에 대해 생각해 보는 것도 재미있을 것입니다. 예를 들어, 원통의 부피를 가장 효율적으로 둘러싸는 높이와 바닥 반경의 비는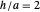 
(즉 바닥의 지름이 높이와 같은)라는 것을 나타내는 것은 간단합니다.
다른 입체를 생각해 볼 수도 있습니다. 여기서는 단순화를 위해 부피를 1로 고정시킵니다.
모든 직육면체 중에서 입방체가 표면적당 가장 큰 부피를 포함합니다.
직각삼각뿔은 데카르트 축을 따라 변의 길이가 같을 때, 둘러싸인 주어진 부피에 대해 최소의 면적을 가집니다.
입체추에서는 표면적을 최소화하는 차원을 닫힘식으로 계산할 수도 있습니다.
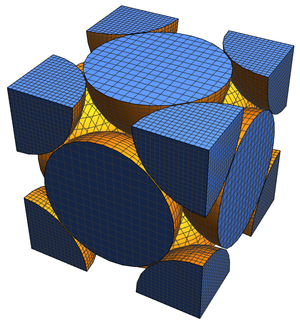
이제 전체적 차원이 변화할 때, 이러한 형태에 대한 가장 효율적인 입체를 시각화할 수 있게 됩니다.
