군관계와 생성원 조사하기
"FiniteGroup" 실체 영역은 주목할만한 유한 차수의 군에 관한 상세 데이터를 보유하고 있습니다.
군의 목록에는 23의 흩어져 있는 군이 포함되어 있으며, 그 중에서 가장 큰 것은 괴물 군입니다. 그 중 첫 번째 일부를 군의 위수와 함께 표로 나타내었습니다.
유한군에서 다수의 재미있는 시각화를 만들 수 있습니다. 간단한 것으로 ArrayPlot을 사용한 곱셈표의 플롯이 있는데, 이것은 기초가 되는 띠와 블록의 구조를 나타냅니다.
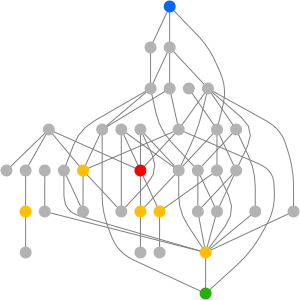
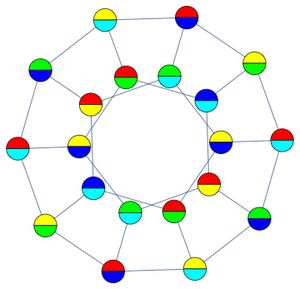
군을 시각화하는 다른 방법으로 케일리(Cayley)그래프가 있습니다. 주어진 그래프와 생성 집합에 관련된 케일리 그래프는 각각의 군의 원소와 연결된 하나의 정점, 및 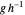 이 생성 집합의 구성원인 경우 항상 유향변
이 생성 집합의 구성원인 경우 항상 유향변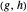 을 가진 유향 그래프로 정의됩니다(케일리 그래프는 생성 집합의 선택에 의존하기도 합니다).
을 가진 유향 그래프로 정의됩니다(케일리 그래프는 생성 집합의 선택에 의존하기도 합니다).
예를 들면, 아벨군 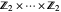 의 케일리 그래프는, 양방향 초입방체 그래프
의 케일리 그래프는, 양방향 초입방체 그래프 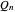 로 주어집니다.
로 주어집니다.
초입방체 그래프와의 대응은 대응하는 초입방체 "Graph" 실체를 반환하는 ToEntity를 통해 확인할 수 있습니다.
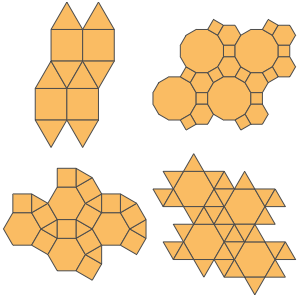
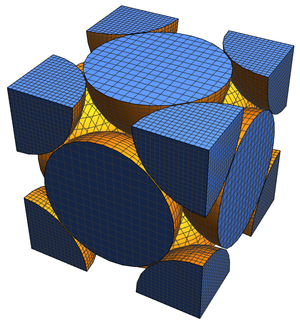
사면체 결정 점군의 케일리 그래프는 준 정다면체 (아르키메데스의 입체) 프레임에서 도출되어 명명된 그래프에 대응합니다.
여기서도 프로그램에서 연상 그래프를 얻을 수 있습니다.
이번에는 이러한 연상 그래를 이 그래프에 대응하는 스켈레톤을 가진 "Polyhedron" 실체 영역의 실체로 변환할 수 있습니다.