함수 공간 조사하기
함수 공간은 집합 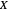 에서 집합
에서 집합 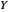 까지 주어진 종류의 함수의 집합입니다. 공간이라고 불리는 것은 많은 분야에서 그것이 위상 공간이며 또한 측도 공간과 관련되어 있는 경우가 많기 때문입니다.
까지 주어진 종류의 함수의 집합입니다. 공간이라고 불리는 것은 많은 분야에서 그것이 위상 공간이며 또한 측도 공간과 관련되어 있는 경우가 많기 때문입니다.
함수 공간은 매우 일반적이고 추상적인 위상 개념에 관계되는 경향이 있습니다. "FunctionSpace" 실체 영역은 125 이상의 공간의 특성을 부호화 가능한 계산적인 형식에서 이용할 수 있도록합니다.
예를 들어, 르베그(Lebesgue) 공간은 유한 차원의 벡터 공간에 대한 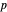 -노름의 자연스러운 일반화를 사용하여 정의됩니다.
-노름의 자연스러운 일반화를 사용하여 정의됩니다. 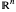 상의 차수
상의 차수 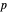 의 르베그 공간의 특성 요약은 Wolfram|Alpha의 쿼리에서 직접 얻을 수 있으며, 여기서는 가장 중요한 포드만을 표시하도록 사용자 정의 되어 있습니다.
의 르베그 공간의 특성 요약은 Wolfram|Alpha의 쿼리에서 직접 얻을 수 있으며, 여기서는 가장 중요한 포드만을 표시하도록 사용자 정의 되어 있습니다.
영역과 측도 공간에 기초하여 정의되는 르베그 공간에는 다수의 변형이 있습니다.
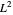 공간의 특수한 경우를 고려해봅니다. 그 노름은 다음과 같이 정의됩니다.
공간의 특수한 경우를 고려해봅니다. 그 노름은 다음과 같이 정의됩니다.
여기서 아직 Wolfram 언어에 포함되지 않은 수학 객체의 자리 표시자로 PureMath 컨텍스트가 사용됩니다.
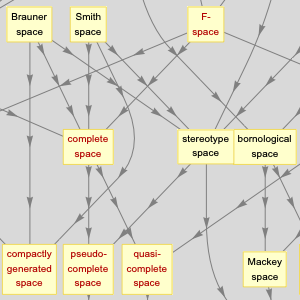
각 공간을 연구한 유명인에 대한 정보를 이용할 수 있습니다.
간편함을 위해 각각의 공간에 사용되는 표기의 표 형식을 제공합니다.
이 실체 영역에 대한 정보가 어떻게 사용되는지에 대한 예로서 간단한 계산을 몇 개 해봅니다.
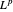 (
(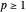 일 때)의 이중 공간을 알아봅니다.
일 때)의 이중 공간을 알아봅니다.
여기서 이중 공간 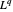 에서 두 수를 가지고 결과의 파라미터화된 실체로 기호 간략화를 실시합니다.
에서 두 수를 가지고 결과의 파라미터화된 실체로 기호 간략화를 실시합니다.
이것은 원래의 공간에 동일하므로 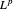 는 회귀적, 즉
는 회귀적, 즉 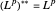 임을 알 수 있습니다.
임을 알 수 있습니다.
이것을 직접 계산할 수도 있습니다.
공간에 대한 보다 자세한 정보는 "TypesetDescription" 특성으로 제공됩니다. 회귀적 공간의 경우, 이 특성은 유용한 추가 설명과 함께 다음과 같은 심층적 정의를 제공합니다.