期待値におけるランダム過程のサポートの向上 

Mathematica 10でランダム過程と確率・統計フレームワークの統合が改良されたことにより，過程の多数のスライスを含む記号計算ができるようになった．特に以下の例では，絶対自己相関関数の2つの推定器を調査し，推定器の偏りとその母分散の間のトレードを調べる．

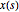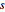を時間 におけるランダム過程arma の値とする．

In[1]:=

X arma\[ScriptCapitalP] = ARMAProcess[{2/5}, {1/5}, 4/3]; \[ScriptCapitalN] = 25;

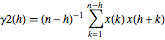絶対相関関数列の2つのサンプル推定器 および を考える．

In[2]:=

X \!\(\*OverscriptBox[\(\[Gamma]1\), \(^\)]\) = Table[1/\[ScriptCapitalN] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(s = 0\), \(\[ScriptCapitalN] - 1 - h\)]\(x[s]\ x[s + h]\)\), {h, 0, \[ScriptCapitalN] - 1}];

In[3]:=

X \!\(\*OverscriptBox[\(\[Gamma]2\), \(^\)]\) = Table[1/(\[ScriptCapitalN] - h) \!\( \*UnderoverscriptBox[\(\[Sum]\), \(s = 0\), \(\[ScriptCapitalN] - 1 - h\)]\(x[s]\ x[s + h]\)\), {h, 0, \[ScriptCapitalN] - 1}];

ARMA(1,1)過程に対するこれらの推定器の母集団期待値を計算する．

In[4]:=

X est1mean = Expectation[ \!\(\*OverscriptBox[\(\[Gamma]1\), \(^\)]\), x \[Distributed] arma\[ScriptCapitalP]];

In[5]:=

X est2mean = Expectation[ \!\(\*OverscriptBox[\(\[Gamma]2\), \(^\)]\), x \[Distributed] arma\[ScriptCapitalP]];

最初の推定器 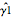には偏りがあるが，2つ目の 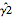にはない．

In[6]:=

X est1mean == AbsoluteCorrelationFunction[ arma\[ScriptCapitalP], {\[ScriptCapitalN] - 1}]["Values"]

Out[6]=

In[7]:=

X est2mean == AbsoluteCorrelationFunction[ arma\[ScriptCapitalP], {\[ScriptCapitalN] - 1}]["Values"]

Out[7]=

これらの推定器の母分散を計算する．

In[8]:=

X AbsoluteTiming[est1var = Expectation[( \!\(\*OverscriptBox[\(\[Gamma]1\), \(^\)]\) - est1mean)^2, x \[Distributed] arma\[ScriptCapitalP]];]

Out[8]=

In[9]:=

X AbsoluteTiming[est2var = Expectation[( \!\(\*OverscriptBox[\(\[Gamma]2\), \(^\)]\) - est2mean)^2, x \[Distributed] arma\[ScriptCapitalP]];]

Out[9]=

不偏推定器の分散は大きな遅れに対して大きくなる．

In[10]:=

X ListPlot[{est1var, est2var}, PlotLegends -> {"Biased", "Unbiased"}]

Out[10]=

従ってAbsoluteCorrelationFunctionは偏りのある推定器を使う．

In[11]:=

X AbsoluteCorrelationFunction[ Table[x[s], {s, 0, \[ScriptCapitalN] - 1}], {\[ScriptCapitalN] - 1}] == \!\(\*OverscriptBox[\(\[Gamma]1\), \(^\)]\)

Out[11]=