Suporte aprimorado para processos aleatórios em expectativa
A integração aprimorada para processos aleatóreos e os frameworks de estatística e probabilidade do Mathematica 10 permitem computação simbólica com muitas fatias de um processo. Em particular, esse exemplo investiga dois estimadores da função de autocorrelação absoluta e explora as trocas entre o viés do estimador e sua variância de população.
Seja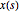 
que denota valores de um processo aleatório arma no tempo 
.
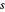| In[1]:= |  X |
Considere dois estimadores de amostra da sequência de função de correlação absoluta—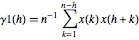 
e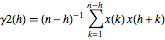 
.
| In[2]:= |  X |
| In[3]:= |  X |
Compute expectativa de população desses estimadores para um processo ARMA(1,1).
| In[4]:= |  X |
| In[5]:= |  X |
O primeiro estimador,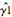 
, é enviesado, enquanto o segundo, 
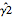, não é.
| In[6]:= |  X |
| Out[6]= |  |
| In[7]:= |  X |
| Out[7]= |  |
Compute variâncias de população desses estimadores.
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |
A variância do estimador não enviesado aumenta para grandes atrasos.
| In[10]:= |  X |
| Out[10]= |  |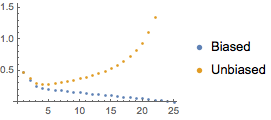
Consequentemente, AbsoluteCorrelationFunction usa o estimador enviesado.
| In[11]:= |  X |
| Out[11]= |  |
