对期望值的随机过程支持的改进
Mathematica 10 中改进的对随机过程和概率以及统计框架的整合,使对许多过程切片进行符号计算成为可能. 特别是在以下范例中,对两个绝对自相关函数的估计量进行研究,调查估计量的偏差和其总体方差间的权衡.
用 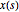 在时间
在时间 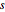 表示随机过程 arma 的值.
表示随机过程 arma 的值.
| In[1]:= | X |
设想绝对相关函数序列的样本估计量: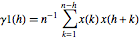 和
和 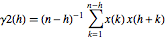 .
.
| In[2]:= | X |
| In[3]:= | X |
对于 ARMA(1,1) 过程,计算这两个估计器总体期待值.
| In[4]:= | X |
| In[5]:= | X |
第一个 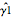 是有偏估计量,但是第二个
是有偏估计量,但是第二个 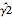 是无偏估计量.
是无偏估计量.
| In[6]:= | X |
| Out[6]= |
| In[7]:= | X |
| Out[7]= |
计算这两个估计器的总体方差.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |
无偏估计量的方差产生更大的延迟.
| In[10]:= | X |
| Out[10]= | 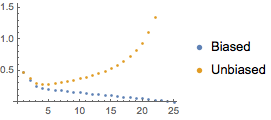 |
因此,AbsoluteCorrelationFunction 使用有偏估计量.
| In[11]:= | X |
| Out[11]= |
























