Soporte mejorado de procesos aleatorios en Expectation
La integración mejorada de Mathematica 10 de procesos aleatorios y marcos de probabilidad y estadística, permite la computación simbólica con muchas porciones de un proceso. En particular, este ejemplo investiga dos estimadores de la función absoluta de autorrelación y explora el intercambio entre el sesgo del estimador y su varianza de población.
Deje que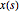 
denote valores de un proceso aleatorio arma en tiempo 
.
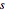| In[1]:= |  X |
Considere un estimador de dos muestras de una secuencia de función absoluta de correlación: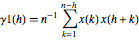 
and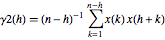 
.
| In[2]:= |  X |
| In[3]:= |  X |
Calcule la expectativa de población de estos estimadores para un proceso ARMA(1,1).
| In[4]:= |  X |
| In[5]:= |  X |
El primer estimador,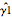 
, es sesgado, mientras el segundo, 
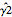, no lo es.
| In[6]:= |  X |
| Out[6]= |  |
| In[7]:= |  X |
| Out[7]= |  |
Calcule las varianzas de población de estos estimadores.
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |
La varianza de un estimador sin sesgo crece para grandes rezagos.
| In[10]:= |  X |
| Out[10]= |  |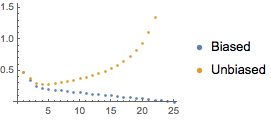
Entonces, AbsoluteCorrelationFunction usa el estimador sesgado.
| In[11]:= |  X |
| Out[11]= |  |
