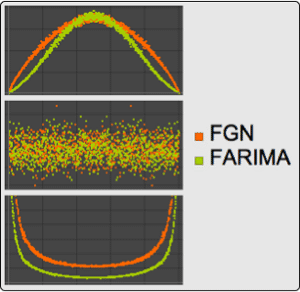
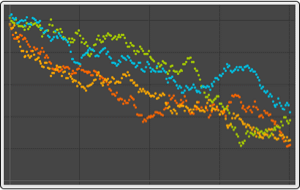
Improved Support of Random Processes in Probability
Find the probability of Poisson process slice 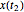 assuming a particular value, given process slice values at an earlier and a later time.
assuming a particular value, given process slice values at an earlier and a later time.
| In[2]:= | X |
| Out[2]= |
| In[3]:= | X |
| Out[3]= |
Compare the probability to PDF of binomial distribution.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
Find the probability of binomial process slice 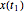 assuming a particular value, given process slice value at a later time.
assuming a particular value, given process slice value at a later time.
| In[7]:= | X |
| Out[7]= |
Compare the probability to PDF of hypergeometric distribution.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |