Auf serielle Korrelation testen
Generieren Sie eine Zufallsstichprobe eines ARProcess.
| In[1]:= | X |
Die geschätzte Korrelationsfunktion nimmt langsam ab als eine Funktion über Zeit.
| In[2]:= | X |
| Out[2]= | 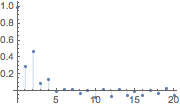 |
Testen Sie auf serielle Korrelation bis zum Lag 10.
| In[3]:= | X |
| Out[3]= |  |
Der Tests bestätigt, dass die Daten eine serielle Korrelation aufweisen.
| In[4]:= | X |
| Out[4]= |  |
Generieren Sie nun die Zufallsstichprobe eines GARCHProcess.
| In[5]:= |  X |
Die Werte der geschätzten Korrelationsfunktion bei Lags ungleich Null sind sehr klein.
| In[6]:= | X |
| Out[6]= | 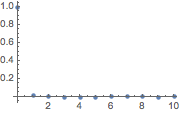 |
Überprüfen Sie den ersten Pfad mit AutocorrelationTest.
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |  |
Es liegt keine serielle Korrelation vor, aber die Abschnitte sind nicht unabhängig.
| In[9]:= | X |
| In[10]:= | X |
Überprüfen Sie die Unabhängigkeit zwischen dem Abschnitt zum Zeitpunkt Null und die vier folgenden Abschnitte mit dem Hoeffdingschen Unabhängigkeitstest .
| In[11]:= | 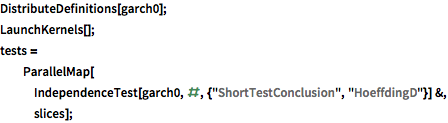 X |
Erzeugen Sie Streudiagramme der Werte der jeweiligen Abschnitte zum Zeitpunkt Null und zu anderen Zeiten, um die aus dem Test gewonnenen Folgerungen zu veranschaulichen.
| Out[12]= | 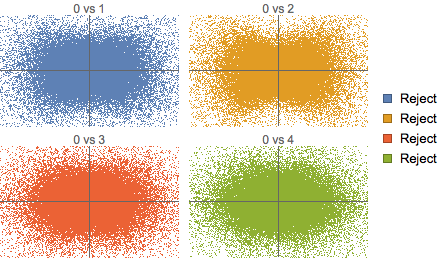 |

























