Prueba de correlación serial
Genere una muestra al azar de un ARProcess.
| In[1]:= | X |
La función de correlación estimada disminuye lentamente como una función de retardo.
| In[2]:= | X |
| Out[2]= | 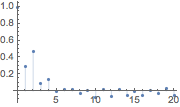 |
Prueba de correlación serial hasta retraso 10.
| In[3]:= | X |
| Out[3]= |  |
Las pruebas confirman que los datos se correlacionan en serie.
| In[4]:= | X |
| Out[4]= |  |
Ahora genere una muestra al azar a partir de un GARCHProcess.
| In[5]:= |  X |
Los valores de la función de correlación estimada con retardos distintos de cero son muy pequeños.
| In[6]:= | X |
| Out[6]= | 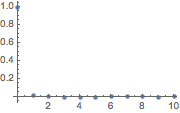 |
Verifique la primer ruta con el AutocorrelationTest.
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |  |
No hay correlación en serie, pero las porciones no son independientes.
| In[9]:= | X |
| In[10]:= | X |
Verifique la independiencia entre la porción en tiempo cero y las siguientes cuatro porciones usando la prueba de independiencia de Hoeffding.
| In[11]:= |  X |
Muestre diagramas de dispersión de valores de porción en tiempo cero y en otros tiempos y las conclusiones de la prueba.
| Out[12]= | 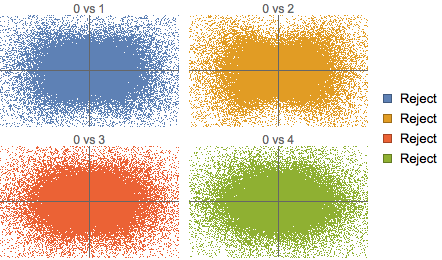 |

























