Neu in Mathematica 10 › Erweiterte Zeitreihenprozesse ›

Erwartungswert eines ARMA-Prozesses anhand seiner Definition berechnen 

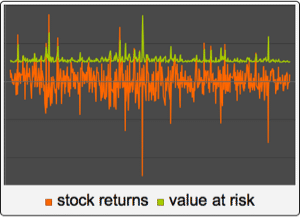
Dieses Beispiel untersucht einen ARMA (Autoregressive-Moving Average)-Prozess mit Anfangswerten. Prozesswerte werden je nach Folge der Innovationen konstruiert. Dieses Beispiel nutzt die verbesserte Unterstützung von Zufallsprozessen mit der Expectation-Funktion, um den Mittelwert und die Kovarianz der Prozessabschnitte zu berechnen. Außerdem wird der stationäre Zeitreihenprozess re-interpretiert als Zeitreihenprozess mit zufälligen Anfangswerten.

Definieren Sie ARMA-Prozesswerte anhand der definierenden Beziehung als eine Funktion zur Bestimmung der vom weißen Rauschen erzeugten Prozesswerte .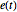

In[1]:=
Click for copyable input
X
Out[1]=

Verarbeiten Sie Werte für den ARMA(2,1)-Prozess.

In[2]:=
Click for copyable input
X

Berechnen Sie das Mittel der Prozesswerte 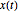wenn 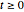, sowie bestimmte vergangene Prozesswerte und bestimmte Nullwerte der Innovationen in der Vergangenheit.

In[3]:=
Click for copyable input
X
In[4]:=
Click for copyable input
X
Out[4]=

Vergleichen Sie dies mit den Werten, die sich aus der Mittelwertsfunktion des Prozesses ergeben.

In[5]:=
Click for copyable input
X
Out[5]=

Berechnen Sie mit dem Expectation-Befehl die Kovarianzfunktion der Prozesswerte unter denselben Bedingungen.

In[6]:=
Click for copyable input
X
Out[6]//Short=

Die Kovarianzfunktion für einen bestimmten Wert der Prozessparameter.

In[7]:=
Click for copyable input
X
Out[7]//MatrixForm=

Vergleichen Sie die berechnete Kovarianzmatrix mit Werten der CovarianceFunction.

In[8]:=
Click for copyable input
X
Out[8]=

Berechnen Sie das Mittel und die Kovarianz der Prozesswerte in der Annahme einer Gaußschen multivariaten Normalverteilung vergangener Werte und vergangener Innovationen.

In[9]:=
Click for copyable input
X
In[10]:=
Click for copyable input
X
In[11]:=
Click for copyable input
X
Out[11]=
In[12]:=
Click for copyable input
X
Out[12]//Short=

Eine schwache Stationaritätsbedingung impliziert, dass die Mittelwerte gleich und die Werte der Kovarianzmatrix in den Subdiagonalen dieselben sein sollten. Dies bestimmt Parameter der multivariaten Verteilung vergangener Werte.

In[13]:=
Click for copyable input
X
Out[13]=

Vergleichen Sie dies mit der Kovarianzfunktion des schwach stationären ARMA(2,1)-Prozesses.

In[14]:=
Click for copyable input
X
Out[14]=

Related Examples

Decide Time Series Process Family and Order from Data Automatically » Identify Conditional Heteroscedacity » Airline Passengers » Constrain the Model Selection Set »
Use Different Criteria for Model Selection » Investigate Time Series Model Residuals » Study Significance of Parameters in Fitted Model » Use Fitted Model to Forecast Time Series »
Model Multiple Exchange Rates » Vector Joint Model versus Univariate Component Models » Use Vector Models with Multiple Strongly Correlated Time Series » Vector Autoregressive Process as Discretized Vector Ornstein–Uhlenbeck Process »
Time Series Processes with Nonzero Mean » Time Series Processes with Initial Conditions » Study Non-weakly Stationary Autoregressive Process » Compute Expectation of Autoregressive Moving-Average Process from Its Definition »
Use Spectral Estimator to Find FARIMA Parameters » Volatility Clustering in a GARCHProcess » Slice Distribution of GARCH(1,1) » Moments of GARCH(1,1) »
Model the Conditional Value at Risk with an ARCHProcess » Expanded Estimation Methods » Broad Performance Improvements »
en es ja pt-br zh