Calcule la expectativa de un proceso autorregresivo promedio en movimiento desde su definición
Este ejemplo explora un proceso ARMA con valores iniciales. Este construye valores de proceso en términos de la secuencia de innovaciones y utiliza soporte mejorado de procesos aleatorios en Expectation para calcular la media y covarianza de segmentos del proceso. Además, el procesos de series temporales estacionario es reinterpretado como proceso de series temporales con valores iniciales aleatorios.
Defina valores de proceso autorregresivo promedio en movimiento a través de su relación de definición como una función de conducción de valores de proceso de ruido blanco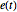 
.
| In[1]:= |  X |
| Out[1]= |  |
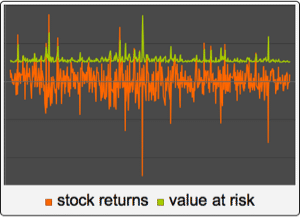
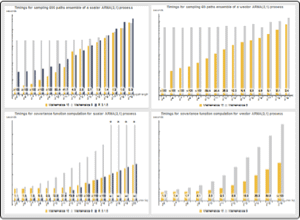
Valores de proceso para proceso ARMA(2,1).
| In[2]:= |  X |
Calcule la media de valores de proceso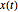 
para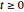 
, dados los valores de proceso pasados, y dados los valores cero de innovaciones en el pasado.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |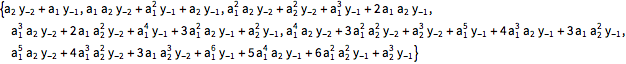
Compare con los valores de la función media de proceso.
| In[5]:= |  X |
| Out[5]= |  |
Utilice Expectation para calcular la función de covarianza de valores de proceso bajo las mismas condiciones.
| In[6]:= |  X |
| Out[6]//Short= | |
 | |
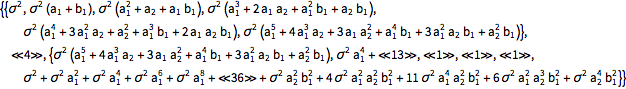La función de covarianza para un valor particular de parámetros de proceso.
| In[7]:= |  X |
| Out[7]//MatrixForm= | |
 | |
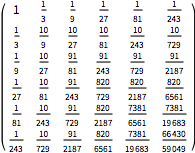Compare la matriz de covarianza computada con valores de CovarianceFunction.
| In[8]:= |  X |
| Out[8]= |  |
Calcule la media y covarianza de valores de proceso asumiendo una distribución de articulaciones gaussiana para valores e innovaciones pasados.
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= | 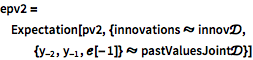 X |
| Out[11]= |  |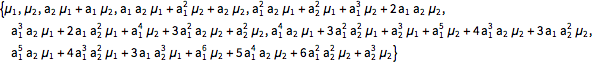
| In[12]:= |  X |
| Out[12]//Short= | |
 | |
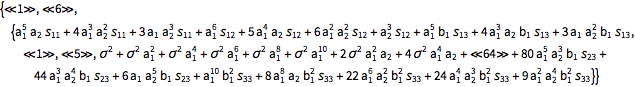Una condición estacionaria débil implica que los valores medios deberían ser iguales y los valores de la matriz de covarianza entre sub-diagonales deben ser los mismos. Esto determina los parámetros de una distribución de articulaciones de valores pasados.
| In[13]:= |  X |
| Out[13]= |  |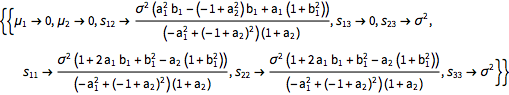
Compare con la función de covarianza de un proceso estacionario débil ARMA(2,1).
| In[14]:= |  X |
| Out[14]= |  |
