Compute expectativa de processo de média móvel autorregressivo a partir de sua definição
Este exemplo explora um processo ARMA com valores iniciais. Ele constrói valores de processo em termos da sequência de inovações e usa suporte avançado de processos aleatórios em Expectation para calcular a média e a covariância das fatias do processo. Além disso, o processo de série temporal estacionária é reinterpretado como processo de série temporal com valores iniciais aleatórios.
Defina valores de processo de média móvel autorregressivo através de sua relação de definição como uma função de direcionamento de valores de processo de ruído branco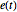 
.
| In[1]:= |  X |
| Out[1]= |  |
Processe valores para o ARMA(2,1).
| In[2]:= |  X |
Compute a média de valores de processo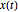 
para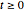 
, dados valores de processo do passado, e considerando as inovações no passado como sendo zero.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |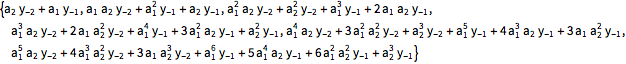
Compare aos valores da função média do processo.
| In[5]:= |  X |
| Out[5]= |  |
Use Expectation para computar a função de covariância dos valores do processo sob as mesmas condições.
| In[6]:= |  X |
| Out[6]//Short= | |
 | |
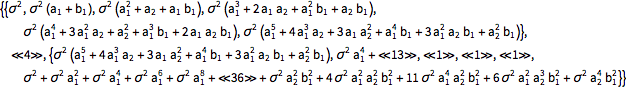Função de covariância para um valor particular de parâmetros do processo.
| In[7]:= |  X |
| Out[7]//MatrixForm= | |
 | |
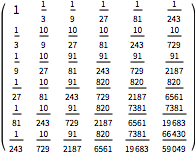Compare a matriz de covariância computada aos valores da CovarianceFunction.
| In[8]:= |  X |
| Out[8]= |  |
Calcule a média e a covariância dos valores do processo assumindo uma distribuição conjunta Gaussiana para valores passados e inovações passadas.
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= | 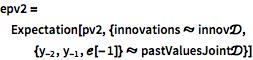 X |
| Out[11]= |  |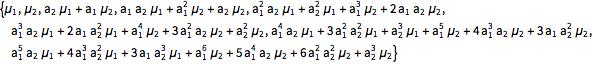
| In[12]:= |  X |
| Out[12]//Short= | |
 | |
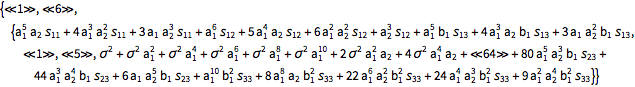A condição de estacionariedade fraca implica que os valores médios devem ser iguais e os valores da matriz de covariância através de subdiagonais devem ser os mesmos. Isso determina os parâmetros da distribuição conjunta de valores passados.
| In[13]:= |  X |
| Out[13]= |  |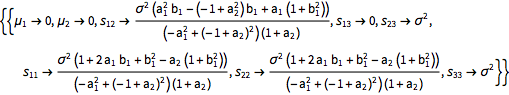
Compare com a função de covariância do processo ARMA(2,1) fracamente estacionário.
| In[14]:= |  X |
| Out[14]= |  |
