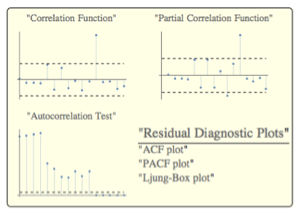
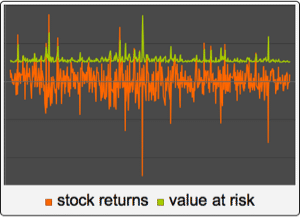
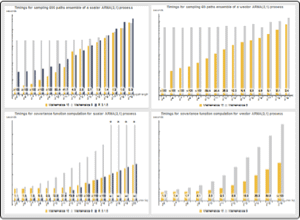
自己回帰移動平均過程の定義から，その期待値を計算する
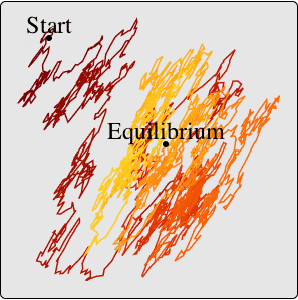
この例では初期値を持つARMA過程を調べる．これは一連のイノベーションについての過程値を構築し，Expectationにおいて向上したランダム過程のサポートを使って過程のスライスの平均と共分散を計算する．定常時系列過程はランダムな初期値を持つ時系列過程として再解釈される．
定義関係を使って，ホワイトノイズ過程の値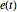 
を発生させる関数として自己回帰移動平均過程の値を定義する．
| In[1]:= |  X |
| Out[1]= |  |
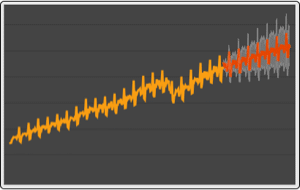
ARMA(2,1)過程の過程値．
| In[2]:= |  X |
過去の過程値が与えられ，過去のイノベーションのゼロ値が与えられた場合に，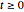
での過程値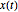 
の平均を計算する．
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |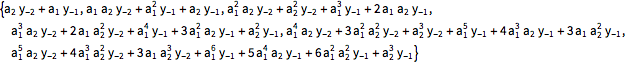
過程の平均関数の値と比較する．
| In[5]:= |  X |
| Out[5]= |  |
Expectationを使って，同じ条件下での過程値の共分散関数を計算する．
| In[6]:= |  X |
| Out[6]//Short= | |
 | |
過程母数の特定の値に対する共分散関数．
| In[7]:= |  X |
| Out[7]//MatrixForm= | |
 | |
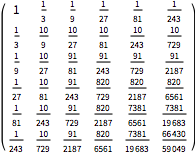計算された共分散行列をCovarianceFunctionの値と比較する．
| In[8]:= |  X |
| Out[8]= |  |
過去の値と過去のイノベーションに対するガウスの結合分布を仮定して，過程値の平均と共分散を計算する．
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= | 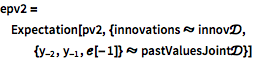 X |
| Out[11]= |  |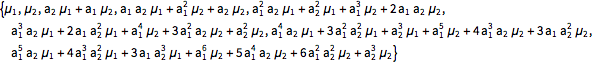
| In[12]:= |  X |
| Out[12]//Short= | |
 | |
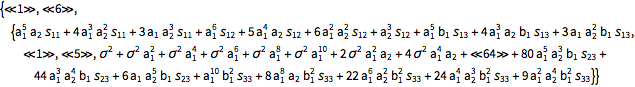弱定常条件は平均値が等しく，対角要素の一つ下にある成分全体の共分散行列値が等しいことを意味する．これにより，過去の値の結合分布の母数が決定される．
| In[13]:= |  X |
| Out[13]= |  |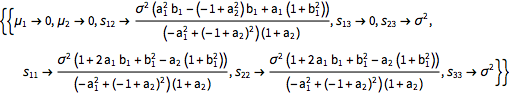
弱定常のARMA(2,1)過程の共分散関数と比較する．
| In[14]:= |  X |
| Out[14]= |  |
