用自回归移动平均过程的定义计算其期望值
该范例对一个有初始值的 ARMA 过程进行研究. 它根据新息序列构建过程值，并用 Expectation 中对随机过程的增强支持，计算过程切片的均值和协方差. 此外，将时间序列过程重新诠释为有随机初始值的时间序列.
通过其关系定义，将自回归移动平均过程的值定义为驱动白噪声过程值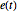 
的函数.
| In[1]:= |  X |
| Out[1]= |  |
ARMA（2,1）过程的过程值.
| In[2]:= |  X |
计算当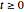 
时，过程值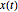 
的均值，给定过去过程值，且给定过去的新息值为零.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |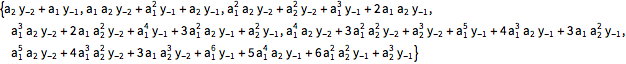
与过程均值函数值相比较.
| In[5]:= |  X |
| Out[5]= |  |
在相同条件下，用 Expectation 计算过程值的协方差函数.
| In[6]:= |  X |
| Out[6]//Short= | |
 | |
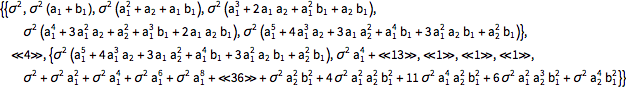过程参数的特定值的协方差函数.
| In[7]:= |  X |
| Out[7]//MatrixForm= | |
 | |
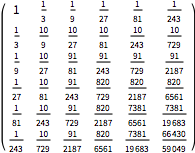将 CovarianceFunction 的值与计算的协方差矩阵相比较.
| In[8]:= |  X |
| Out[8]= |  |
假定过去值和新息为高斯联合分布，计算过程值的均值和协方差.
| In[9]:= |  X |
| In[10]:= |  X |
| In[11]:= | 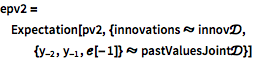 X |
| Out[11]= |  |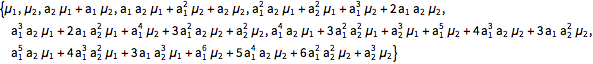
| In[12]:= |  X |
| Out[12]//Short= | |
 | |
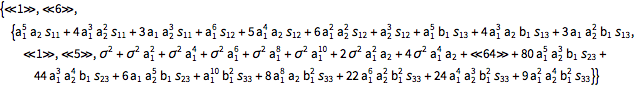弱平稳条件意味着平均值应相等，且所有次对角的协方差矩阵值也应该相同. 这决定了过去值的联合分布的参数.
| In[13]:= |  X |
| Out[13]= |  |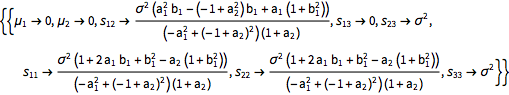
与弱平稳 ARMA（2,1）过程的协方差函数相比较.
| In[14]:= |  X |
| Out[14]= |  |
