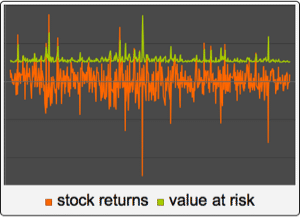
Der vektorielle autoregressive Prozess als diskretisierter vektorieller Ornstein–Uhlenbeck-Prozess 

Die verbesserte Unterstützung für Berechnungen mit einfachen Prozessabschnitten sowie für Zeitreihenprozesse mit beliebigen Mittelwerten und mit Anfangswerten ermöglicht das Matching eines einheitlich diskretisierten Gaußschen Itô-Prozesses mit einem vektoriellen autoregressiven Prozess (VAR).

Definieren Sie einen 2D-Itô-Prozess mit linearen Driftkoeffizienten und konstanten Diffusionskoeffizienten.

In[1]:=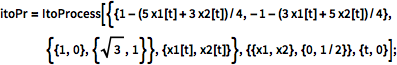

X itoPr = ItoProcess[{{1 - (5 x1[t] + 3 x2[t])/ 4, -1 - (3 x1[t] + 5 x2[t])/4}, {{1, 0}, {Sqrt[3], 1}}, {x1[t], x2[t]}}, {{x1, x2}, {0, 1/2}}, {t, 0}];

Definieren Sie einen bivariaten autoregressiven Prozess mit Anfangswerten.

In[2]:=

X varPr = ARProcess[{c1, c2}, {{{a11, a12}, {a21, a22}}}, {{s1, s12}, {s12, s2}}, {{x10ar, x20ar}}];

Da es sich bei beiden Prozessen um Gaußsche Prozesse handelt, werden beide vollständig über ihre Mittelwerte und Kovarianzfunktionen bestimmt.

In[3]:=

X itoPrmf[t_] = Mean[itoPr[t]];

In[4]:=

X itoPrcovF[s_, t_] = Simplify[CovarianceFunction[itoPr, s, t]];

In[5]:=

X varPrmf[n_] = Mean[varPr[n]];

In[6]:=

X varPrcovF[n_, m_] = Simplify[CovarianceFunction[varPr, n, m]];

Erstellen Sie Momentengleichungen, indem Sie die die Momentenfunktion des Itô-Prozesses in regelmäßigen Zeitintervallen und die VAR-Momentenfunktion zu konsekutiven ganzen Zahlen aufstellen.

In[7]:=

X dt = 1/1000;

In[8]:=

X meanEqs = Table[itoPrmf[n dt] == varPrmf[n - 1], {n, 4}]; covEqs = Table[ Flatten[itoPrcovF[n dt, m dt]] == Flatten[varPrcovF[n - 1, m - 1]], {n, 4}, {m, n, 4}];

Lösen Sie die Gleichungen.

In[9]:=

X {sol} = NSolve[ Join[meanEqs, Flatten[covEqs]], {c1, c2, x10ar, x20ar, a11, a12, a21, a22, s1, s2, s12}]

Out[9]=

Die Simulation des VAR-Prozesses ergibt die exakte Simulation des Itô-Prozesses in einem regelmäßigen Gitter.

In[10]:=

X path = RandomFunction[varPr /. sol, {0, 20000}]

Out[10]=

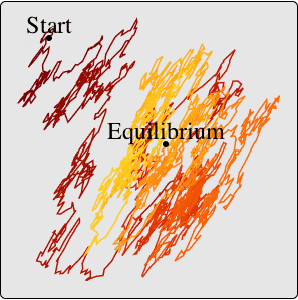
Visualisieren Sie den Pfad.

Die gesamte Wolfram-Language Eingabe zeigenEingabe verbergen

In[11]:=

X Legended[Graphics[{{Gray, Line[path["Values"]]}, {Red, PointSize[.03], Point[{x10ar, x20ar} /. sol]}, {Orange, PointSize[.03], Point[Limit[itoPrmf[t], t -> Infinity]]} }, AspectRatio -> 1, Frame -> True, ImageSize -> Medium], LineLegend[{Red, Orange, Gray}, {"starting point", "stationary mean", "process path"}, Joined -> {False, False, True}]]

Out[11]=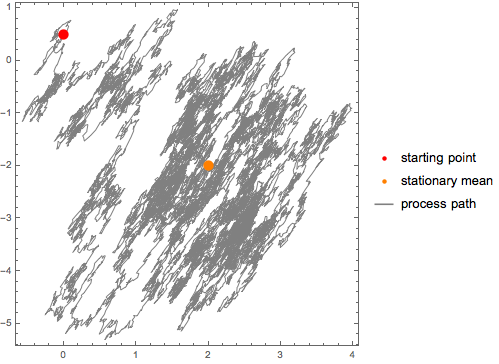