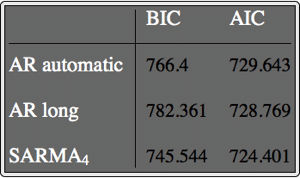
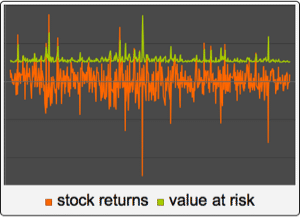
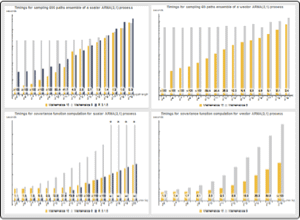
離散化されたベクトルオルンシュタイン・ウーレンベック過程としてのベクトル自己回帰過程
過程のスライスの計算のサポートが向上し,初期値を持つ任意平均の時系列過程および時間過程がサポートされるようになったことで,一様に離散化されたガウス伊藤過程をベクトル値の自己回帰過程にマッチさせることが可能になった.
線形ドリフト係数と定数拡散係数を持つ2Dの伊藤過程を定義する.
| In[1]:= | 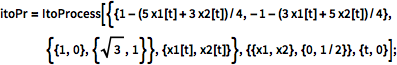 X |
初期値を持つ二変量自己回帰過程を定義する.
| In[2]:= | X |
どちらの過程もガウス過程なので,平均および共分散関数により完全に指定することができる.
| In[3]:= | X |
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | X |
等間隔の時間における伊藤過程のモーメント関数と,連続整数におけるVARのモーメント関数を同等と見なすことにより,モーメントの方程式を構築する.
| In[7]:= | X |
| In[8]:= |  X |
方程式を解く.
| In[9]:= | X |
| Out[9]= |
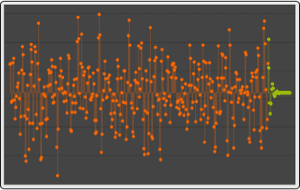
VAR過程のシミュレーションで,規則格子の伊藤過程の厳密なシミュレーションが得られる.
| In[10]:= | X |
| Out[10]= |
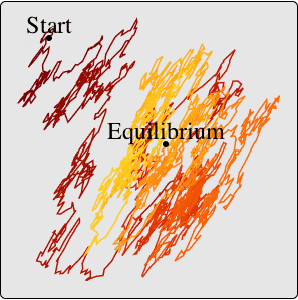
経路を可視化する.
| Out[11]= | 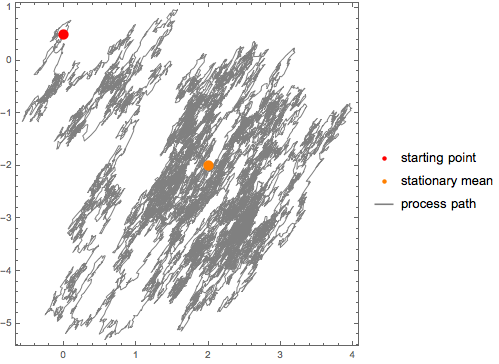 |