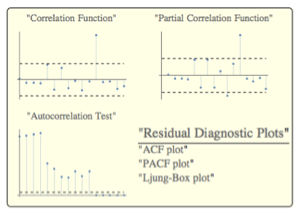
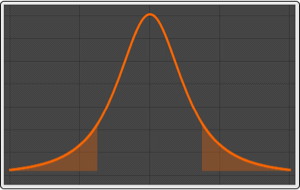
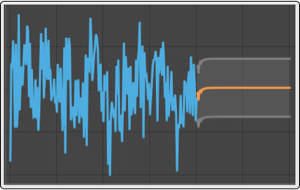
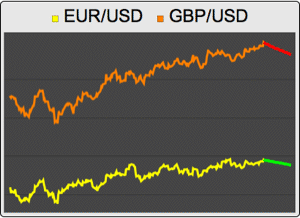
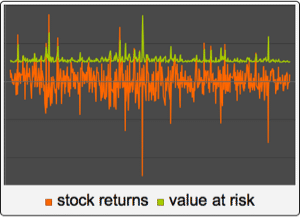
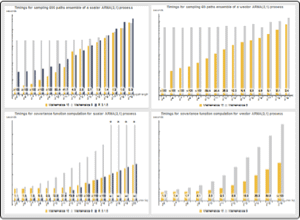
作为离散向量 Ornstein–Uhlenbeck 过程的向量自回归过程 

对计算过程切片的提高，以及对任意均值时间序列过程和有初始值的时间序列的支持，可以将均匀离散的高斯伊藤过程对向量值自回归过程进行匹配.

定义一个有线性漂移系数和恒量扩散系数的二维伊藤过程.

In[1]:=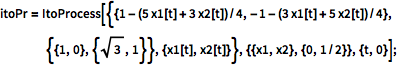

X itoPr = ItoProcess[{{1 - (5 x1[t] + 3 x2[t])/ 4, -1 - (3 x1[t] + 5 x2[t])/4}, {{1, 0}, {Sqrt[3], 1}}, {x1[t], x2[t]}}, {{x1, x2}, {0, 1/2}}, {t, 0}];

定义一个有初始值的双变量自回归过程.

In[2]:=

X varPr = ARProcess[{c1, c2}, {{{a11, a12}, {a21, a22}}}, {{s1, s12}, {s12, s2}}, {{x10ar, x20ar}}];

由于两个都是高斯过程，可以用均值和协方差函数进行指定.

In[3]:=

X itoPrmf[t_] = Mean[itoPr[t]];

In[4]:=

X itoPrcovF[s_, t_] = Simplify[CovarianceFunction[itoPr, s, t]];

In[5]:=

X varPrmf[n_] = Mean[varPr[n]];

In[6]:=

X varPrcovF[n_, m_] = Simplify[CovarianceFunction[varPr, n, m]];

通过将等间隔时间的伊藤过程矩函数和连续整数的 VAR 矩函数进行等值，构建矩的方程.

In[7]:=

X dt = 1/1000;

In[8]:=

X meanEqs = Table[itoPrmf[n dt] == varPrmf[n - 1], {n, 4}]; covEqs = Table[ Flatten[itoPrcovF[n dt, m dt]] == Flatten[varPrcovF[n - 1, m - 1]], {n, 4}, {m, n, 4}];

解方程.

In[9]:=

X {sol} = NSolve[ Join[meanEqs, Flatten[covEqs]], {c1, c2, x10ar, x20ar, a11, a12, a21, a22, s1, s2, s12}]

Out[9]=

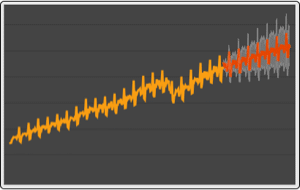
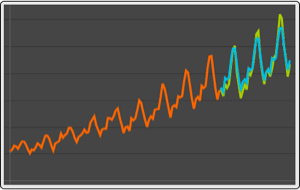
对 VAR 过程的模拟给出了对规则网格的伊藤过程的精确模拟.

In[10]:=

X path = RandomFunction[varPr /. sol, {0, 20000}]

Out[10]=

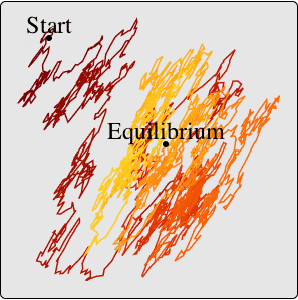
可视化路径.

显示完整的 Wolfram 语言输入隐藏输入

In[11]:=

X Legended[Graphics[{{Gray, Line[path["Values"]]}, {Red, PointSize[.03], Point[{x10ar, x20ar} /. sol]}, {Orange, PointSize[.03], Point[Limit[itoPrmf[t], t -> Infinity]]} }, AspectRatio -> 1, Frame -> True, ImageSize -> Medium], LineLegend[{Red, Orange, Gray}, {"starting point", "stationary mean", "process path"}, Joined -> {False, False, True}]]

Out[11]=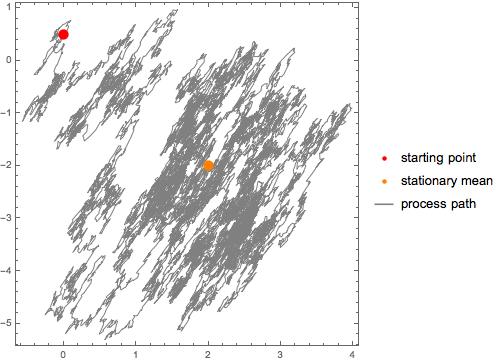