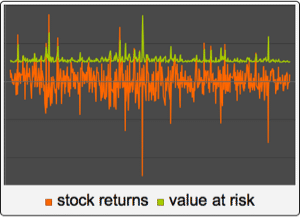
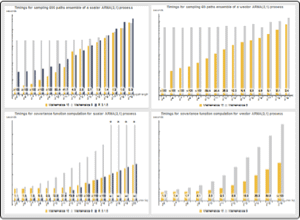
GARCHProcessにおけるボラティリティクラスタリング 

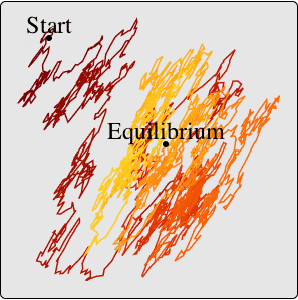
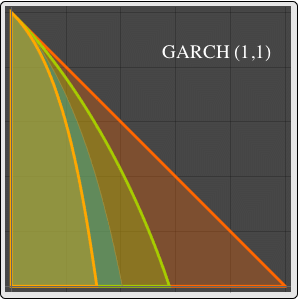
一般化された自己回帰条件付き分散不均一過程GARCHProcessは，ボラティリティクラスタリング現象を示す時系列を記述するために使われる．大きい変化の後にはどちらかの符号の大きい変化が続き，小さい変化の後には小さい変化が続く傾向がある．

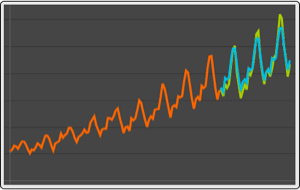
GARCHProcessのシミュレーションを実行する．

In[1]:=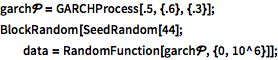

X garch\[ScriptCapitalP] = GARCHProcess[.5, {.6}, {.3}]; BlockRandom[SeedRandom[44]; data = RandomFunction[garch\[ScriptCapitalP], {0, 10^6}]];

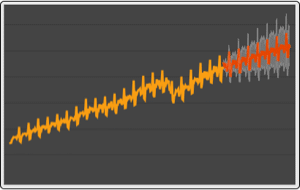
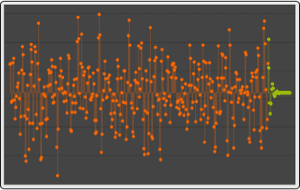
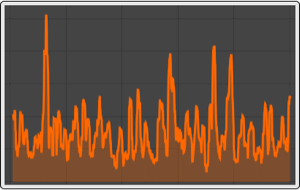
長さ10のウィンドウで移動標準偏差をプロットする．

In[2]:=

X var = MovingMap[StandardDeviation, data, 10]; ListLinePlot[TimeSeriesResample[var, 100], PlotRange -> {0, 40}, Ticks -> {Table[{10^5 k, k}, {k, 10}], Automatic}, AxesLabel -> {"\[Times] 10^5", None}, ImageSize -> Medium]

Out[2]=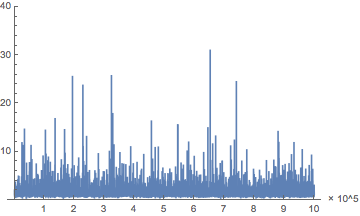

過程の前の時間の値が指定された数値に近いものとして，標準偏差を計算する関数を定義する．

完全なWolfram言語入力を表示する入力を隠す

In[3]:=

X cfBinarySearch = Compile[{{list, _Real, 1}, {elem, _Real}}, Module[{n0 = 1, n1 = Length[list], m = 1, lm}, While[n0 < n1, m = Quotient[n0 + n1, 2]; lm = Part[list, m]; If[lm == elem, Break[]]; If[lm < elem, n0 = m + 1, n1 = m - 1]]; m], RuntimeOptions -> "Speed", RuntimeAttributes -> Listable];

In[4]:=

X condVar[pd_, v_] := Module[{cd, n, var, p0, p1}, {p0, p1} = cfBinarySearch[pd[[All, 1]], v + Abs[v] {-0.1, 0.1}]; cd = Take[pd, {p0 - 1, p1}]; n = Length[cd]; If[n > 10, {Mean[cd[[All, 1]]], StandardDeviation[cd[[All, 2]]]}, {Indeterminate, Indeterminate}]]

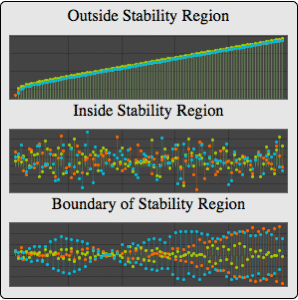
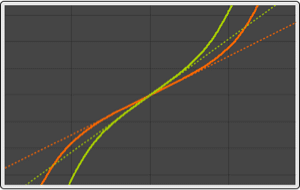
条件付き標準偏差を条件付き値の関数として推定する．

In[5]:=

X Quantile[data, {0, 0.01, 0.05, 0.95, 0.99, 1}]

Out[5]=

In[6]:=

X vlist = Join[#, -#] &[{1, 2, 4, 6, 8, 10, 15, 20, 25, 30, 35, 40}]; Block[{pd = SortBy[Partition[data["Values"], 2, 1], First]}, sdEst = Table[condVar[pd, v], {v, Sort[vlist]}]];

In[7]:=

X ListLinePlot[SortBy[sdEst, First]]

Out[7]=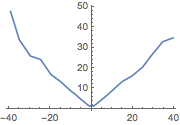

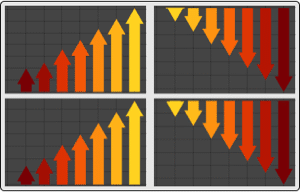
ARMA過程のサンプルのグラフと比較する．この過程の条件付き標準偏差は一定である．

In[8]:=

X arma\[ScriptCapitalP] = ARMAProcess[{.6, 0.1}, {.3}, 1]; BlockRandom[SeedRandom[44]; data2 = RandomFunction[arma\[ScriptCapitalP], {10^6}]];

In[9]:=

X Quantile[data2, {0, 0.01, 0.05, 0.25, 0.75, 0.95, 0.99, 1}]

Out[9]=

In[10]:=

X vlist = Join[#, -#] &[{0.5, 1, 2, 3, 4, 5}]; Block[{pd2 = SortBy[Partition[data2["Values"], 2, 1], First]}, sdEst2 = Table[condVar[pd2, v], {v, Sort[vlist]}]];

In[11]:=

X ListLinePlot[SortBy[sdEst2, First], PlotRange -> {0, 2}]

Out[11]=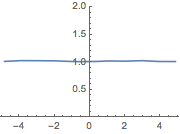