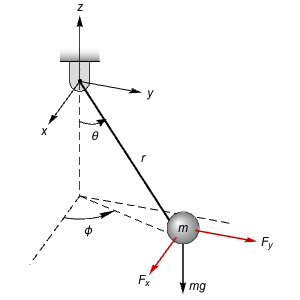
漸近出力追従 

連続撹はん槽反応器の液体量と製品濃度を指定された値で維持するフィードバック制御器を設計する． »

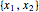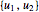状態と入力のアフィン系．

In[1]:=

X pars = {Subscript[c, B1] -> 20.05, Subscript[c, B2] -> 0.2, Subscript[k, 1] -> 0.4, Subscript[k, 2] -> 1};

In[2]:=

X asys = AffineStateSpaceModel[ {{-Subscript[k, 1] Sqrt[Subscript[x, 1]], -((Subscript[k, 2] Subscript[x, 2])/(1 + Subscript[x, 2])^2)}, {{ 1, 1 }, {( Subscript[c, B1] - Subscript[x, 2])/Subscript[x, 1], ( Subscript[c, B2] - Subscript[x, 2])/Subscript[x, 1] }}, {Subscript[ x, 1], Subscript[x, 2]}, {{ 0, 0 }, {0, 0 }}}, {{Subscript[x, 1], 25.05}, {Subscript[x, 2], 9}}, {{Subscript[u, 1], 1}, {Subscript[u, 2], 1}}, {Automatic, Automatic}, Automatic , SamplingPeriod -> None];

目的は，エラー崩壊率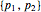で出力を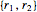に維持することである．

In[3]:=

X pars1 = {Subscript[r, 1] -> 30, Subscript[r, 2] -> 10.5, Subscript[p, 1] -> -1, Subscript[p, 2] -> -1.5};

目的を達成するフィードバック制御器．

In[4]:=

X fb = AsymptoticOutputTracker[ asys, {Subscript[r, 1], Subscript[r, 2]}, {Subscript[p, 1], Subscript[p, 2]}]

Out[4]=

閉ループ系．

In[5]:=

X csys = SystemsModelStateFeedbackConnect[asys, fb] /. pars /. pars1

Out[5]=

追従を確認するために閉ループ系をシミュレーションする．

In[6]:=

X OutputResponse[csys, {0, 0}, {t, 0, 4}];

In[7]:=

X OutputResponse[csys, {0, 0}, {t, 0, 4}];; Plot[Evaluate[ Join[%, {Subscript[r, 1], Subscript[r, 2]} /. pars1]], {t, 0, 4}, PlotStyle -> {Automatic, Automatic, Dashed, Dashed}, PlotLegends -> {"liquid level", "product concentration", "ref. liquid level", "ref. product concentration"}]

Out[7]=

制御努力．

In[8]:=

X pars = {Subscript[c, B1] -> 20.05, Subscript[c, B2] -> 0.2, Subscript[k, 1] -> 0.4, Subscript[k, 2] -> 1};; Plot[Evaluate[ Join[%, {Subscript[r, 1], Subscript[r, 2]} /. pars1]], {t, 0, 4}, PlotStyle -> {Automatic, Automatic, Dashed, Dashed}, PlotLegends -> {"liquid level", "product concentration", "ref. liquid level", "ref. product concentration"}]; -fb /. Thread[{Subscript[x, 1], Subscript[x, 2]} -> StateResponse[csys, {0, 0}, {t, 0, 4}]] /. pars /. pars1; Plot[Evaluate[%], {t, 0, 4}, PlotRange -> All, AxesOrigin -> {0, 0}, PlotLegends -> {"input 1", "input 2"}]

Out[8]=