Evaluate a Linear Controller Design Using Nonlinear Simulation 

Starting with a nonlinear model, design a linear controller and evaluate the performance of the controller on the nonlinear system.

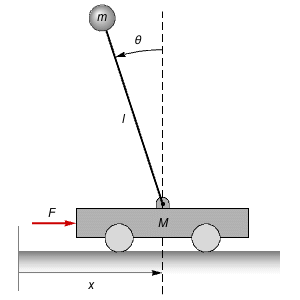
The model of an inverted pendulum is nonlinear, but linear in the input force .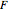

In[1]:=

X eqns = {(M + m) x''[t] + m l Sin[\[Theta][t]] \[Theta]'[t]^2 - m l Cos[\[Theta][t]] \[Theta]''[t] == F[t], l \[Theta]''[t] - x''[t] Cos[\[Theta][t]] - g Sin[\[Theta][t]] == 0};

In[2]:=

X pars = {l -> 1, m -> 0.2, M -> 0.3, g -> 9.8};

In[3]:=

X pend = AffineStateSpaceModel[ eqns, {\[Theta][t], x[t]}, {F[t]}, {\[Theta][t], x[t]}, t]

Out[3]=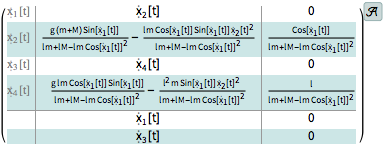

Design a controller based on the linear model.

In[4]:=

X k = StateFeedbackGains[ StateSpaceModel[pend /. pars], {-2, -3 + I, -3 - I, -4}]

Out[4]=

Connect the linear controller to the nonlinear model.

In[5]:=

X csys = SystemsModelStateFeedbackConnect[pend, k]

Out[5]=

Simulate the nonlinear closed-loop system.

In[6]:=

X res = OutputResponse[{csys /. pars, {40 \[Degree], 0, 0, 0}}, 0, {t, 0, 4}];

In[7]:=

X Plot[res, {t, 0, 4}, PlotRange -> All, PlotLegends -> {\[Theta][t], x[t]}]

Out[7]=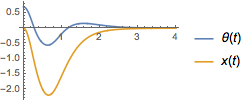